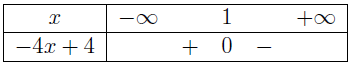Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Hôm nay, mình sẽ hướng dẫn các bạn cách tìm điểm uốn của một đồ thị hàm số bất kỳ.
Trong phạm vị ngắn gọn của bài viết này, mình sẽ trình bày trực tiếp với bạn về khái niệm điểm uốn chứ không trình bày gián tiếp thông qua cung lồi và cung lõm nữa.
Việc tìm điểm uốn của đồ thị hàm số ngoài ngoài đáp ứng yêu cầu của bài toán còn giúp chúng ta vẽ đồ thị hàm số được chính xác và đẹp mắt.
Mục Lục Nội Dung
I. Điểm uốn là gì?
Điểm $U\left(x_0 ; f\left(x_0\right)\right)$ được gọi là điểm uốn của đồ thị hàm số $y=f(x)$ nếu tồn tại một khoảng $(a ; b)$ chứa điểm $x_0$…
Sao cho, trên một trong hai khoảng $\left(a ; x_0\right)$ và $\left(x_0 ; b\right)$ tiếp tuyến của đồ thị tại điểm $U$ nằm phía trên đồ thị, còn trên khoảng kia tiếp tuyến nằm phía dưới đồ thị.
Lúc này, người ta nói rằng tiếp tuyến tại điểm uốn xuyên qua đồ thị.
II. Làm thế nào để tìm điểm uốn của đồ thị?
Để tìm được điểm uốn của đồ thị thì bạn có thể sử dụng nội dung của khẳng định đã được chứng minh sau đây:
Nếu hàm số $y=f(x)$ có đạo hàm cấp hai trên một khoảng chứa điểm $x_0$, $f^{\prime \prime}\left(x_0\right)=0$ và $f^{\prime \prime}(x)$ đổi dấu khi $x$ qua điểm $x_0$ thì $U\left(x_0 ; f\left(x_0\right)\right)$ là một điểm uốn của đồ thị hàm số $y=f(x)$
III. Bài tập tìm điểm uốn của đồ thị hàm số
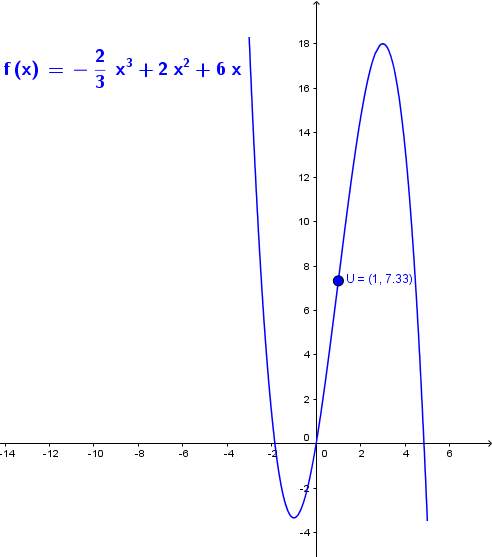
Ví dụ 1. Tìm điểm uốn của đồ thị hàm số $f(x)=-\frac{2}{3} x^3+2x^2+6x$
Lời giải:
$f^{\prime}(x)=-2x^2+4x+6$ suy ra $f^{\prime \prime}(x)=-4x+4$
Cho $f^{\prime \prime}(x)=0$ chúng ta được phương trình $-4x+4=0 \Leftrightarrow x=1$
Bảng xét dấu $f^{\prime \prime}(x)=-4x+4$
Vì $f^{\prime \prime}(x)$ đổi dấu từ dương sang âm khi $x$ qua điểm $1$ nên $U\left(1 ; \frac{22}{3}\right)$ là điểm uốn của đồ thị hàm số đã cho.
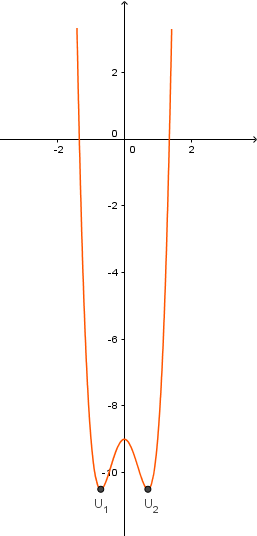
Ví dụ 2. Tìm điểm uốn của đồ thị hàm số $y=6x^4-6x^2-9$
Lời giải:
$y^{\prime}=24x^3-12x$ suy ra $y^{\prime \prime}=72x^2-12$
Cho $y^{\prime \prime}=0$ chúng ta được phương trình $72x^2-12=0$
Dễ thấy $y^{\prime \prime}=0$ tại các điểm $x_1=\frac{\sqrt{6}}{6}, x_2=-\frac{\sqrt{6}}{6}$
Bảng xét dấu $y^{\prime \prime}=72x^2-12$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Quan sát bảng xét dấu chúng ta nhận thấy $y^{\prime \prime}$ đổi dấu khi $x$ qua mỗi điểm $x_1$ và $x_2$
Vậy $U_1\left(-\frac{\sqrt{6}}{6} ;-\frac{59}{6}\right)$ và $U_2\left(\frac{\sqrt{6}}{6} ;-\frac{59}{6}\right)$ là hai điểm uốn của đồ thị hàm số đã cho.
IV. Mẹo tìm điểm uốn của một số hàm số đặc biệt
Chúng ta có thể tìm nhanh điểm uốn của hàm số bậc ba và hàm số trùng phương theo các chỉ dẫn bên dưới:
#1. Đối với hàm số bậc ba
Các nhà Toán học đã chứng minh được đồ thị của hàm số bậc ba $f(x)=a x^3+b x^2+c x+d$ với $a \neq 0$ luôn có một điểm uốn và điểm đó là tâm đối xứng của đồ thị.
#2. Đối với hàm số trùng phương
Gọi $(\mathscr{C})$ là đồ thị của hàm số $f(x)=a x^4+b x^2+c$ với $a \neq 0$
Các nhà Toán học đã chứng minh được rằng:
- Nếu phương trình $f^{\prime \prime}(x)=0$ có hai nghiệm phân biệt $x=\pm x_0$ $(x_0>0)$ thì đồ thị $(\mathscr{C})$ có hai điểm uốn $U_1\left(x_0 ; f\left(x_0\right)\right)$ và $U_2\left(-x_0 ; f\left(-x_0\right)\right)$ đối xứng với nhau qua trục tung
- Nếu phương trình $f^{\prime \prime}(x)=0$ có một nghiệm kép hoặc vô nghiệm thì đồ thị $(\mathscr{C})$ không có điểm uốn.
V. Lời kết
Muốn tìm điểm uốn của đồ thị hàm số một cách nhanh chóng và chính xác nhất thì ngoài các kiến thức vừa được trình bày bên trên, các bạn nên xem thêm hoặc xem lại bài viết:
- Công thức tính đạo hàm
- Cách giải phương trình bậc nhất, bậc hai, bậc ba
- Cách xét dấu nhị thức, tam thức
Cuối cùng, đừng quên mẹo tìm nhanh điểm uốn của hàm số bậc ba và hàm số trùng phương mà mình vừa chia sẻ ở trên.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
