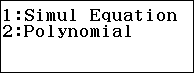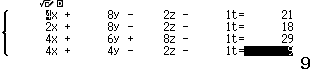Cách viết phương trình mặt cầu (2 trường hợp)

Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách viết phương trình mặt cầu trong không gian !

Tương tự với cách viết phương trình đường tròn trên mặt phẳng, mình cũng sẽ hướng dẫn cho các bạn hai trường hợp thường gặp nhất (đó là khi biết tâm và bán kính, biết bốn điểm đi qua).

Trước khi bắt đầu tìm hiểu, nếu có thể thì bạn hãy chuẩn bị máy tính CASIO fx-580VN X trước (có link phía dưới), hoặc cài giả lập trên máy tính cũng được. Chúng ta sẽ cần đến nó để giải nhanh hệ bốn phương trình bậc nhất bốn ẩn bạn nhé !

#1. Viết phương trình mặt cầu khi biết tâm và bán kính

Người ta đã chứng minh được một phương trình mặt cầu hoàn toàn xác định khi biết tâm và bán kính của nó.

Phương trình mặt cầu tâm $I=(x_0; y_0; z_0)$ và bán kính R sẽ là $(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$

Ví dụ 1. Viết phương trình mặt cầu biết tâm $I=(2; 3; 5)$ và bán kính $R=7$

Lời giải:

Phương trình mặt cầu cần tìm có dạng $(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$

Vì phương trình này có tâm $I=(2; 3; 5)$ và bán kính $R=7$ nên ta được $(x-2)^2+(y-3)^2+(z-5)^2=49$

Vậy => phương trình mặt cầu cần tìm là $(x-2)^2+(y-3)^2+(z-5)^2=49$

Ví dụ 2. Viết phương trình mặt cầu đi qua hai điểm $A=(2; 3; 5)$ và $B=(7; 11; 13)$ và nhận đoạn thẳng AB làm đường kính.

Lời giải:

Tọa độ tâm của mặt cầu cần tìm là $\left(\frac{2+7}{2}; \frac{3+11}{2}; \frac{5+13}{2}\right)$ hay $\left(\frac{9}{2}; 7; 9\right)$

Bán kính của mặt cầu cần tìm là $\frac{\sqrt{(7-2)^2+(11-3)^2+(13-5)^2}}{2}=\frac{3\sqrt{17}}{2}$

Vậy => phương trình mặt cầu cần tìm là $\left(x-\frac{9}{2}\right)^2+(y-7)^2+(z-9)^2=\frac{153}{4}$

#2. Viết phương trình mặt cầu khi biết bốn điểm đi qua

Phương trình mặt cầu $(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$ còn có thể viết dưới dạng khai triển là $x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+d=0$ với $d=x_0^2+y_0^2+z_0^2-R^2$

Khi được yêu cầu viết phương trình mặt cầu đi qua bốn điểm chúng ta sẽ sử dụng phương trình ở dạng khai triển

Giả sử phương trình mặt cầu cần tìm đi qua bốn điểm $A=(x_a; y_a; z_a), B=(x_b; y_b; z_b), C=(x_c; y_c; z_c), D=(x_d; y_d; z_d)$

Bước 1. Lần lượt thay tọa độ bốn điểm A, B, C, D vào phương trình khai triển ta sẽ được hệ bốn phương trình bậc nhất bốn ẩn:

$\left\{\begin{array}{ll}x_a^2+y_a^2+z_a^2-2x_0x_a-2y_0y_a-2z_0z_a+d&=0\\x_b^2+y_b^2+z_b^2-2x_0x_b-2y_0y_b-2z_0z_b+d&=0\\x_c^2+y_c^2+z_c^2-2x_0x_c-2y_0y_c-2z_0z_c+d&=0\\x_d^2+y_d^2+z_d^2-2x_0x_d-2y_0y_d-2z_0z_d+d&=0\end{array}\right.$

Bước 2. Sử phương phương pháp thế, phương pháp cộng, … để giải hệ này ta sẽ tìm được nghiệm $x_0, y_0, z_0, d$

Bước 3. Thay $x_0, y_0, z_0, d$ vào phương trình $x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+d=0$  chúng ta sẽ được một phương trình mặt cầu

Chú ý:

• Các cụm từ bốn điểm thuộc mặt cầu, bốn điểm nằm trên mặt cầu, mặt cầu đi qua bốn điểm là cùng một nghĩa
• Có vô số phương trình mặt cầu đi qua ba điểm

Ví dụ 3. Viết phương trình mặt cầu đi qua bốn điểm $A(2; 4; -1), B(1; 4; -1), C(2; 3; 4), D(2; 2; -1)$

Lời giải:

Phương trình mặt cầu cần tìm có dạng $x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+d=0$ và đi qua bốn điểm $A(2; 4; -1), B(1; 4; -1), C(2; 3; 4), D(2; 2; -1)$ nên ta được hệ phương trình:

$\left\{\begin{array}{ll}2^2+4^2+(-1)^2-2x_02-2y_04-2z_0(-1)+d&=0\\1^2+4^2+(-1)^2-2x_01-2y_04-2z_0(-1)+d&=0\\2^2+3^2+4^2-2x_02-2y_03-2z_04+d&=0\\2^2+2^2+(-1)^2-2x_02-2y_02-2z_0(-1)+d&=0\end{array}\right.$

$ \Leftrightarrow \left\{\begin{array}{ll}-4x_0-8y_0+2z_0+d&=-21\\-2x_0-8y_0+2z_0+d&=-18\\-4x_0-6y_0-8z_0+d&=-29\\-4x_0-4y_0+2z_0+d&=-9\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x_0&=\frac{3}{2}\\y_0&=3\\z_0&=\frac{7}{5}\\d&=\frac{31}{5}\end{array}\right.$

Vậy => phương trình đường mặt cầu tìm là $x^2+y^2+z^2-3x-6y-\frac{14}{5}z+\frac{31}{5}=0$

#3. Thủ thuật viết nhanh phương trình mặt cầu đi qua 4 điểm bằng máy tính CASIO

Nền tảng của thủ thuật này chính là phương trình $x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+d=0$ và phương thức tính toán Equation / Func

Ví dụ 4. Phương trình mặt cầu đi qua bốn điểm $A(2; 4; -1), B(1; 4; -1), C(2; 3; 4), D(2; 2; -1)$ là

1. $x^2+y^2+z^2-3x-6y-\frac{14}{5}z+\frac{31}{5}=0$
2. $x^2+y^2+z^2+3x-6y-\frac{14}{5}z+\frac{31}{5}=0$
3. $x^2+y^2+z^2-3x+6y-\frac{14}{5}z+\frac{31}{5}=0$
4. $x^2+y^2+z^2-3x-6y+\frac{14}{5}z+\frac{31}{5}=0$

Các bước thực hiện:

Bước 1. Chọn phương thức tính toán Equation / Func

Bước 2. Chọn Simul Equation

Bước 3. Nhấn phím số 4 trên bàn phím

Bước 4. Nhập các hệ số của hệ phương trình …

• Đối phương trình thứ nhất giá trị các hệ số theo thứ tự sẽ là: hai lần hoành độ điểm thứ nhất, hai lần trung độ điểm thứ nhất, hai lần cao độ điểm thứ nhất, -1, tổng của bình phương hoàng độ, trung độ và cao độ của điểm thứ nhất
• Đối phương trình thứ nhì, thứ ba, thứ tư tương tự.

Bước 5. Nhấn phím = => nhấn phím = => nhấn phím = => nhấn phím =

Vậy phương trình mặt cầu cần tìm là $x^2+y^2+z^2-3x-6y-\frac{14}{5}z+\frac{31}{5}=0$

Đáp án là phương án A

#4. Lời kết

Phương trình đường tròn, phương trình mặt cầu đều là tập hợp các điểm cách đều một điểm cho trước với một khoảng cách cố định cho trước.

Hai phương trình này chỉ khác nhau một chỗ đó là, phương trình đường tròn thì nằm trên mặt phẳng, còn phương trình mặt cầu thì nằm trong không gian. Thế thôi !

Có thể nói, phương trình mặt cầu là trường hợp mở rộng của phương trình đường tròn. Nếu tiếp tục mở rộng bạn sẽ thu được một phương trình gọi là phương trình siêu cầu..

Vâng, đó là đôi lời mở rộng kiến thức thay cho lời kết mà mình muốn gửi đến các bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com