Tổng hợp các cách xét vị trí tương đối giữa hai mặt phẳng

Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách xét vị trí tương đối giữa hai mặt phẳng.

Nếu cả hai mặt phẳng đều được cho dưới dạng phương trình tổng quát thì bạn có thể tiến hành xét ngay lập tức.

Trường hợp có một phương trình được cho dưới dạng tham số thì: hoặc là bạn chuyển nó thành dạng tổng quát, hoặc là bạn thay nó vào phương trình tổng quát của mặt phẳng còn lại rồi tiến hành lý luận.

#1. Cách tính định thức của ma trận vuông cấp 2 x 2

$\left|\begin{array}{cc}a&b\\c&d\end{array}\right|$ được gọi là định thức của ma trận vuông cấp 2 x 2 và khai triển của nó là $ad-cb$

#2. Chuyển phương trình mặt phẳng từ dạng tham số sang dạng tổng quát

Trong không gian $Oxyz$, cho mặt phẳng $(P)$ đi qua điểm $M_{0}(x_{0}; y_{0}; z_{0})$ và có cặp vectơ chỉ phương là $\overrightarrow{u_{1}}(a_{1}; b_{1}; c_{1}), \overrightarrow{u_{2}}(a_{2}; b_{2}; c_{2})$

Phương trình tham số của mặt phẳng $(P)$ là $\left\{\begin{array}{ll} x&=x_{0}+a_{1}t_{1}+a_{2}t_{2} \\ y&=y_{0}+b_{1}t_{1}+b_{2}t_{2} \\ z&=z_{0}+c_{1}t_{1}+c_{2}t_{2} \end{array}\right.$, với $t_{1}, t_{2}$ là các tham số

Phương trình tổng quát tương ứng của mặt phẳng $(P)$ là:

$\left|\begin{array}{ccc} x-x_{0} & y-y_{0} & z-z_{0} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|=0 \qquad (*)$

$(*) \Leftrightarrow (x-x_0)\left|\begin{array}{cc}b_1&c_1\\b_2&c_2\end{array}\right|-(y-y_0)\left|\begin{array}{cc}a_1&c_1\\a_2&c_2\end{array}\right|+(z-z_0)\left|\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right|=0$

$(*) \Leftrightarrow (x-x_0)(b_1c_2-b_2c_1)-(y-y_0)(a_1c_2-a_2c_1)+(z-z_0)(a_1b_2-a_2b_1)=0$

#3. Cách xét vị trí tương đối giữa hai mặt phẳng

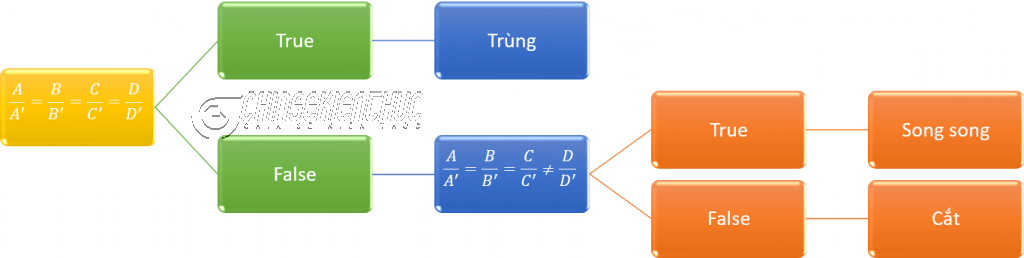
Trong không gian Oxyz cho mặt phẳng (P) và (P’) lần lượt có phương trình tổng quát là $Ax+By+Cz+D=0$ và $A’x+B’y+C’z+D’=0$

• Nếu $\frac{A}{A’}=\frac{B}{B’}=\frac{C}{C’}=\frac{D}{D’}$ thì hai mặt phẳng đã cho trùng nhau.
• Nếu $\frac{A}{A’}=\frac{B}{B’}=\frac{C}{C’}\neq\frac{D}{D’}$ thì hai mặt phẳng đã cho song song với nhau.
• Nếu $(A:B:C) \neq (A’:B’:C’)$ thì hai mặt phẳng đã cho cắt nhau.

#4. Bài tập ví dụ minh họa

Ví dụ 1. Trong không gian Oxyz cho mặt phẳng $(P): 6x+8y+9z+8=0$ và mặt phẳng $(Q): 36x+48y+54z+48=0$

Vị trí tương đối của hai mặt phẳng này là?

Lời giải:

Vì $\frac{6}{36}=\frac{8}{48}=\frac{9}{54}=\frac{8}{48}$ nên hai mặt phẳng đã cho trùng nhau.

Ví dụ 2. Trong không gian Oxyz cho mặt phẳng $(P): \left\{\begin{array}{ll} x&=-1-9t_{1}-3t_{2} \\ y&=7t_{1} \\ z&=7t_{2} \end{array}\right.$ và mặt phẳng $(Q): 14x+18y+6z+9=0$

Vị trí tương đối của hai mặt phẳng này là?

Lời giải:

Cách 1. Biến đổi phương trình tham số thành phương trình tổng quát

Phương trình tổng quát tương ứng của mặt phẳng (P) là $\left|\begin{array}{ccc} x+1 & y & z \\ -9 & 7 & 0 \\ -3 & 0 & 7 \end{array}\right|=0 \Leftrightarrow 49x+63y+21z+49=0$

Vì $\frac{49}{14}=\frac{63}{18}=\frac{21}{6}\neq\frac{49}{9}$ nên hai mặt phẳng đã cho song song với nhau

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Cách 2. Thay phương trình tham số vào phương trình tổng quát

Thay (P) vào (Q) ta được $14(-1-9t_1-3t_2)+18(7t_1)+6(7t_2)+9=0 \Leftrightarrow 0t_1+0t_2-5=0$

Vậy hai mặt phẳng đã cho song song với nhau.

Ví dụ 3. Trong không gian Oxyz cho mặt phẳng $(P): \left\{\begin{array}{ll} x&=-1-2t_{1}-6t_{2} \\ y&=8t_{1} \\ z&=8t_{2} \end{array}\right.$

Và mặt phẳng $(Q): \left\{\begin{array}{ll} x&=-4-4t_{1}-9t_{2} \\ y&=1+4t_{1} \\ z&=1+4t_{2} \end{array}\right.$

Vị trí tương đối của hai mặt phẳng này là?

Lời giải:

Cách 1. Biến đổi phương trình tham số thành phương trình tổng quát

Phương trình tổng quát tương ứng của mặt phẳng (P) là $\left|\begin{array}{ccc} x+1 & y & z \\ -2 & 8 & 0 \\ -6 & 0 & 8 \end{array}\right|=0 \Leftrightarrow 64x+16y+48z+64=0$

Phương trình tổng quát tương ứng của mặt phẳng (Q) là $\left|\begin{array}{ccc} x+4 & y-1 & z-1 \\ -4 & 4 & 0 \\ -9 & 0 & 4 \end{array}\right|=0 \Leftrightarrow 16x+16y+36z+12=0$

Vì $(64:16:48) \neq (16:16:36)$ hay $\frac{64}{16} \neq \frac{16}{16} \neq \frac{48}{36}$ nên hai mặt phẳng đã cho cắt nhau

Cách 2. Thay phương trình tham số vào phương trình tổng quát

Phương trình tổng quát tương ứng của mặt phẳng (P) là $\left|\begin{array}{ccc} x+1 & y & z \\ -2 & 8 & 0 \\ -6 & 0 & 8 \end{array}\right|=0 \Leftrightarrow 64x+16y+48z+64=0$

Thay (Q) vào (P) ta được $64(-4-4t_1-9t_2)+16(1+4t_1)+48(1+4t_2)+64=0 \Leftrightarrow -192t_1-384t_2-128=0$

Vậy hai mặt phẳng đã cho cắt nhau.

#5. Lời kết

Trên đây là những cách xét vị trí tương đối giữa hai mặt phẳng mà bạn nên biết.

Trong bài viết này mình có sử dụng kiến thức của Đại số cao cấp là ma trận và định thức, vậy nên:

• Nếu bạn là sinh viên thì không có vấn đề gì, bạn có thể áp dụng thỏa mái, vì bạn đã được học ma trận và cách tính định thức.
• Nếu bạn là học sinh thì bạn hãy có gắng nhớ công thức nhé, thật ra cũng không quá khó nhớ lắm vì nó có quy luật rồi, bạn hãy nghiền ngẫm rồi nghĩ ra mẹo nhớ cho riêng mình ha.

Hi vọng là những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách viết phương trình mặt cầu (2 trường hợp)
• Cách xét vị trí tương đối của đường thẳng và mặt phẳng
• Hướng dẫn cách xét vị trí tương đối của hai đường thẳng

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn