Cách xét vị trí tương đối của đường thẳng và mặt phẳng

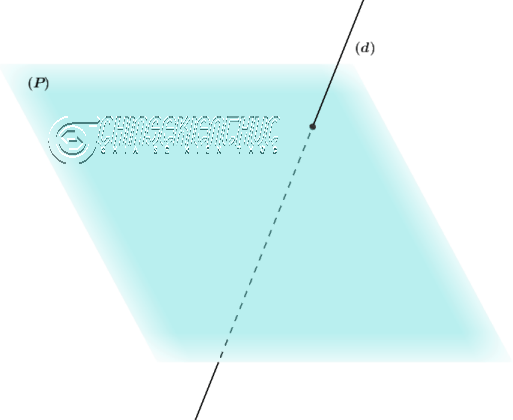
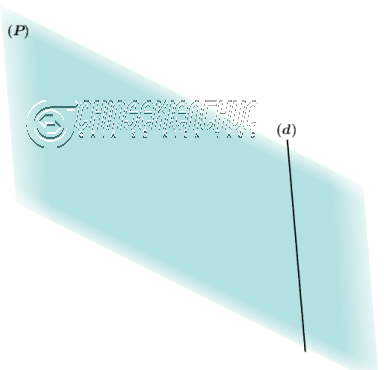
Xin chào tất cả các bạn, hôm nay chúng ta sẽ cùng nhau tìm hiểu cách xét vị trí tương đối của đường thẳng và mặt phẳng.

Đường thẳng ở đây là đường thẳng nằm trong không gian nha các bạn, chúng ta không xét vị trí của đường thẳng nằm trên mặt phẳng.

Việc xét vị trí của đường thẳng và mặt phẳng không có gì khó khăn cả, cơ bản chỉ cần chuyển phương trình đường thẳng thành dạng tham số và thay vào phương trình tổng quát của mặt phẳng là xong.

#1. Chuyển phương trình đường thẳng về dạng tham số

Nếu phương trình đường thẳng được cho dưới dạng chính tắc hoặc tổng quát thì bạn cần chuyển nó về dạng tham số trước khi tiến hành xét vị trí tương đối.

1.1. Chuyển phương trình từ dạng chính tắc sang dạng tham số

Phương trình chính tắc của đường thẳng (d) trong không gian có dạng $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$, với $(x_0; y_0; z_0)$ là điểm đi qua và $(a; b; c)$ là một véc tơ chỉ phương.

Lúc bấy giờ, phương trình tham số tương ứng sẽ có dạng $\left\{\begin{array}{ll}x&=x_0+at\\y&=y_0+bt\\z&=z_0+ct\end{array}\right.$, với t là tham số.

1.2. Chuyển phương trình từ dạng tổng quát sang dạng tham số

Phương trình $\left\{\begin{array}{ll}Ax+By+Cz+D&=0\\A’x+B’y+C’z+D’&=0\end{array}\right.$, với điều kiện là $A^2+B^2+C^2 \neq 0$ và $A’^2+B’^2+C’^2 \neq 0$ được gọi là phương trình tổng quát của đường thẳng (d).

#2. Các bước giải

Bước 1. Chuyển phương trình đường thẳng ở dạng chính tắc hoặc dạng tổng quát về dạng tham số.

Bước 2. Trong không gian Oxyz cho phương trình tham số của đường thẳng (d) và phương trình tổng quát của mặt phẳng (P) lần lượt là:

$\left\{\begin{array}{l}x&=x_{0}+at\\y&=y_{0}+bt\\z&=z_{0}+ ct \end{array}\right.$ và  $Ax+By+Cz+D=0$ thay $(d)$ vào $(P)$ thu gọn ta được $(Aa+Bb+Cc)t+Ax_{0}+By_{0}+Cz_{0}+D=0$

• Nếu $Aa+Bb+Cc \neq 0$ thì $(d)$ cắt $(P)$
• Nếu $Aa+Bb+Cc=0$ và $Ax_{0}+By_{0}+Cz_{0}+D \neq 0$ thì $(d)$ song song $(P)$
• Nếu $Aa+Bb+Cc=0$ và $Ax_{0}+By_{0}+Cz_{0}+D=0$ thì $(d)$ nằm trên $(P)$

#3. Bài tập ví dụ

Ví dụ 1. Xét vị trí tương đối của đường thẳng $(d): \left\{\begin{array}{ll}x&=2-2t\\y&=3+3t\\z&=5-5t\end{array}\right.$ và mặt phẳng $(P):7x-11y+13z-17=0$

Lời giải:

Thay (d) vào (P) ta được $7(2-2t)-11(3+3t)+13(5-5t)-17=0 \Leftrightarrow 29-112t=0$.

Vì $112 \neq 0$ nên (d) và (P) cắt nhau.

Giải phương trình $29-112t=0$ ta được $t=\frac{29}{112}$

Thay $t= \frac{29}{112}$ vào (d) ta được tọa độ giao điểm của (d) và (P) là $(2-2. \frac{29}{112}; 3+3.\frac{29}{112}; 5-5.\frac{29}{112})$ hay $(\frac{83}{56}; \frac{423}{112}; \frac{415}{112})$

Ví dụ 2. Xét vị trí tương đối của đường thẳng $(d): \frac{x-2}{-2}=\frac{y-3}{3}=\frac{z-5}{47}$ và mặt phẳng $(P):7x-11y+z-17=0$

Lời giải:

Dễ thấy phương trình tham số tương ứng của (d) là $\left\{\begin{array}{ll}x&=2-2t\\y&=3+3t\\z&=5+47t\end{array}\right.$

Thay (d) vào (P) ta được $7(2-2t)-11(3+3t)+1(5+47t)-17=0 \Leftrightarrow -31+0t=0$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Vậy => (d) và (P) song song với nhau.

Ví dụ 3. Xét vị trí tương đối của đường thẳng $(d): \left\{\begin{array}{ll}3x+2y-12&=0\\47x+2z-104&=0\end{array}\right.$ và mặt phẳng $(P):7x-11y+z+14=0$

Lời giải:

Cho $z=5$ giải hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{ll}3x+2y&=12\\47x+0y&=94\end{array}\right.$ ta được nghiệm là (2; 3)

Suy ra (2; 3; 5) là một điểm thuộc đường thẳng (d)

Vì $(3:2:0) \neq (47:0:2)$ nên đường thẳng (d) có một véc tơ chỉ phương là $(4; -6; -94)$ hay $(-2; 3; 47)$

Vậy phương trình tham số tương ứng của (d) là $\left\{\begin{array}{ll}x&=2-2t\\y&=3+3t\\z&=5+47t\end{array}\right.$

Thay (d) vào (P) ta được $7(2-2t)-11(3+3t)+1(5+47t)+14=0 \Leftrightarrow 0+0t=0$

Vậy => (d) nằm trên (P)

#4 Lời. kết

Okay, như vậy là qua bài viết này thì bạn đã biết cách xét vị trí tương đối của đường thẳng và mặt phẳng rồi đúng không?!

Bạn có thể kiểm tra lại kết quả bằng cách vẽ đường thẳng và mặt phẳng trong cùng một không gian.

GeoGebra là một trong những ứng cử viên hàng đầu, phần mềm GeoGebra có thể cài được trên điện thoại, máy tính bảng, máy tính và có cả phiên bản trực tuyến nữa.

Ngoài việc kiểm tra kết quả ra thì bạn còn có thể vẽ hình minh họa cho học sinh/ sinh viên của mình (nếu bạn là giáo viên / giảng viên giảng dạy Toán học).

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách viết phương trình mặt cầu (2 trường hợp)
• Cách viết phương trình đường thẳng trong không gian
• 3 cách chứng minh tam giác đồng dạng, có ví dụ dễ hiểu

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com