Xin chào tất cả các bạn, trong bài viết này chúng ta sẽ cùng nhau tìm hiểu kỹ hơn về định nghĩa đường trung bình của tam giác và đường trung bình của hình thang nhé.
Sau khi nắm được định nghĩa thì chúng ta sẽ cùng tìm hiểu về định lý và kết thúc bằng ba ví dụ minh họa để các bạn nhớ được lâu hơn.
Mục Lục Nội Dung
I. Đường trung bình của tam giác
#1. Định nghĩa
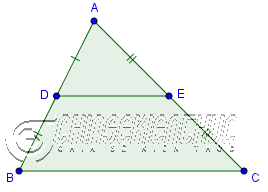
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Như hình bên dưới thì: DE là đường trung bình của tam giác ABC vì D và E lần lượt là trung điểm của cạnh AB và AC
Chú ý: Trong một tam giác bất kỳ luôn có ba đường trung bình.
#2. Định lý
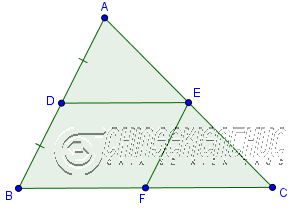
Định lý 1.
Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ 2 thì đi qua trung điểm của cạnh thứ ba.
| Giả thuyết | $\triangle ABC, AD=DB, DE \parallel BC$ |
| Kết luận | $AE=EC$ |
Bạn có thể chứng minh Định lí 1 bằng cách vẽ một đường thẳng đi qua điểm E và song song với cạnh AB, lúc bấy giờ đường thẳng vừa kẻ sẽ cắt BC ở F
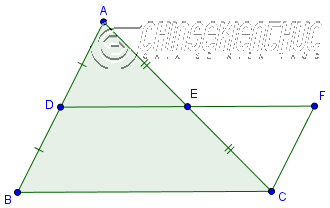
Định lý 2.
Đường trung bình của tam giác sẽ song song với cạnh thứ ba và có độ dài bằng một phần hai độ dài cạnh ấy.
| Giả thuyết | $\triangle ABC, AD=DB, AE=EC$ |
| Kết luận | $DE \parallel BC, DE=\frac{1}{2}BC$ |
Bạn có thể chứng minh Định lí 2 bằng cách vẽ thêm một điểm F sao cho E là trung điểm của DF tức DE = EF
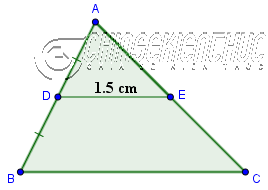
Ví dụ 1. Cho tam giác $ABC$ có $AD=DB, DE \parallel BC$ và $DE=1.5~cm$. Tính độ dài cạnh $BC$
Lời giải:
Vì $AD=DB$ và $DE \parallel BC$ nên $E$ là trung điểm của cạnh $AC$
Suy ra DE là đường trung bình của tam giác $ABC$
Theo giả thuyết chúng ta có $DE=1.5~cm$
Áp dụng Định lí 2 ta được $DE=\frac{1}{2}BC \Leftrightarrow BC=2.DE=2 \times 1.5=3~cm$
Vậy => độ dài cạnh $BC$ bằng $3~cm$
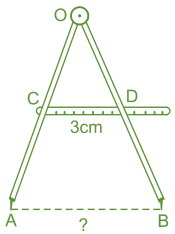
Ví dụ 2. Tính khoảng cách AB giữa hai chân của Compa. Biết C, D lần lượt là trung điểm của OA, OB và $CD=3~cm$
Lời giải:
Vì C, D là trung điểm của AO, BO nên CD là đường trung bình của tam giác AOB
Mặc khác ta có $CD=3~cm$
Áp dụng Định lí 2 ta được $CD=\frac{1}{2}AB \Leftrightarrow AB=2.CD=2.3=6~cm$
Vậy => khoảng cách giữa hai chân của Compa bằng 6 cm
II. Đường trung bình của hình thang
#1. Định nghĩa
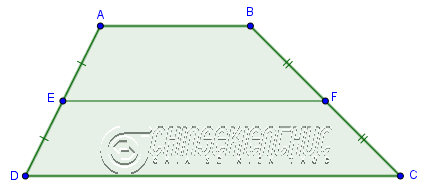
Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh bên của hình thang.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Như hình bên dưới thì: EF là đường trung bình của hình thang ABCD vì E và F lần lượt là trung điểm của cạnh AD và BC
Chú ý: Trong một hình thang bất kì chỉ có duy nhất một đường trung bình.
#2. Định lý
Định lý 3.
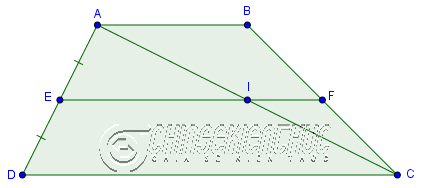
Đường thẳng đi qua trung điểm cạnh bên thứ nhất của hình thang và song song với hai cạnh đáy thì đi qua trung điểm cạnh bên thứ 2.
| Giả thuyết | $ABCD$ là hình thang $(AB \parallel CD)$
$AE=ED, EF \parallel AB, EF \parallel CD$ |
| Kết luận | $BF=FC$ |
Bạn có thể chứng minh Định lí 3 bằng cách vẽ thêm một điểm I sao cho I là giao điểm của AC và EF
Định lý 4.
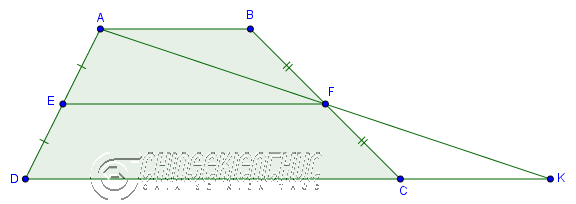
Đường trung bình của hình thang sẽ song song với hai cạnh đáy và có độ dài bằng tổng của nửa độ dài cạnh đáy thứ nhất, nửa độ dài cạnh đáy thứ nhì.
| Giả thuyết | $ABCD$ là hình thang $(AB \parallel CD)$
$AE=ED, BF=FC$ |
| Kết luận | $EF \parallel AB, EF \parallel DC, EF=\frac{AB+DC}{2}$ |
Bạn có thể chứng minh Định lí 4 bằng cách vẽ thêm một điểm K sao cho K là giao điểm của AF và DC
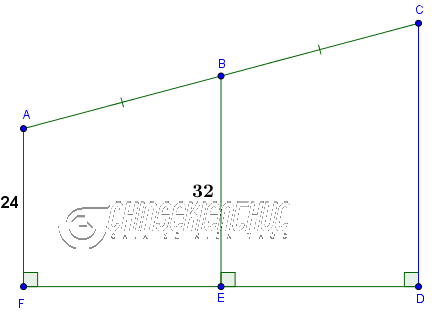
Ví dụ 3. Cho tứ giác $ABCD$ có $AB=BC, AF=24, BE=32, \hat{F}=\hat{E}=\hat{D}=90^o$
Tính độ dài cạnh DC.
Lời giải:
Theo giả thuyết ta có $FA \bot FD$ và $DC \bot EF$ suy ra $FA \parallel DC$
Vậy tứ giác $ACDF$ là hình thang
Cũng theo giả thuyết ta có $AB=BC$ suy ra $B$ là trung điểm $AC$
Mặc khác ta lại có $EB \bot FD$ suy ra $EB \parallel FA$ và $EB \parallel DC$
Vậy $EB$ là đường trung bình của hình thang $ACDF$
Áp dụng Định lí 4 ta được $EB=\frac{FA+DC}{2} \Leftrightarrow DC=2EB-FA=2.32-24=40$
Vậy => độ dài cạnh đáy DC bằng 40 ĐVĐD
III. Lời kết
Đọc đến đây thì mình tin là các bạn đã có thể phát biểu được định nghĩa, định lý và vận dụng giải được một số bài toán cơ bản về đường trung bình của tam giác và đường trung bình của hình thang rồi phải không nào?!
Xa hơn thì bạn có thể vận dụng định lý tính khoảng cách giữa hai địa điểm hoặc hai vật thể (cây, nhà, cột, …) bị ngăn cách bởi chướng ngại vật nào đó (sông, hồ, …). Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha !
Đọc thêm:
- Định nghĩa, tính chất của tam giác (vuông, cân, đều, tù, nhọn…)
- Cách tính diện tích tam giác thường, vuông, cân và tam giác đều
- Cách tính Chu vi và Diện tích của hình thang (có ví dụ dễ hiểu)
- Tứ giác đặc biệt là gì? Định nghĩa, tính chất, dấu hiệu nhận biết..
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống