Định nghĩa, tính chất của tam giác (vuông, cân, đều, tù, nhọn…)

Xin chào tất cả các bạn, trong bài viết này mình sẽ đề cập đến các định nghĩa, cũng như các tính chất cơ bản của các tam giác đặc biệt (như tam giác nhọn, tam giác tù, tam giác vuông, tam giác cân, tam giác vuông cân, tam giác đều).

Mình sẽ phân loại dựa theo độ lớn của các góc hoặc độ dài của các cạnh. Trừ trường hợp tam giác vuông cân. Okay, ngay bây giờ chung ta hãy cùng nhau bắt đầu ha…

#1. Định nghĩa và tính chất của tam giác nhọn

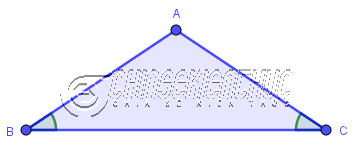
Tam giác có ba góc nhọn (hay nói cách khác là 3 góc có độ lớn nhỏ hơn 90^o) thì được gọi là tam giác nhọn.

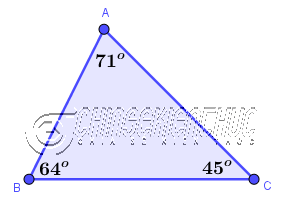
Như hình trên: Tam giác ABC có $\hat{A}=71^o, \hat{B}=64^o, \hat{C}=45^o$ đều nhỏ hơn 90^o nên tam giác ABC là một tam giác nhọn.

#2. Định nghĩa và tính chất của tam giác tù

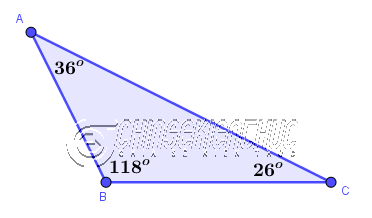
Tam giác có một góc tù (hay nói cách khác là có một góc lớn hơn 90^o) thì được gọi là tam giác tù.

Như hình bên trên: Tam giác ABC có $\hat{B}=118^o$ lớn hơn 90^o nên tam giác ABC là một tam giác tù.

Chú ý: Trong hình học Ơ-clít không tồn tại tam giác có hai góc tù.

#3. Định nghĩa và tính chất của tam giác vuông

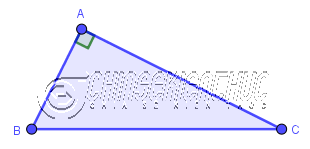
Tam giác có một góc bằng 90^o thì được gọi là tam giác vuông.

Trong hình học Ơ-clít không tồn tại tam giác có hai góc vuông, nếu có ai đó đố bạn vẽ được một tam giác có hai góc vuông thì người đó đang kiểm tra kiến thức của bạn đấy.

Tam giác ABC có góc A bằng 90^o nên tam giác ABC là một tam giác vuông (vuông ở A)

Khi đó …

• AB, AC được gọi là cạnh góc vuông.
• BC được gọi là cạnh huyền.
• $\hat{B}, \hat{C}$ được gọi là góc nhọn.

Trong một tam giác vuông bất kì ta luôn có hai góc nhọn phụ nhau (hay nói cách khác là nó có tổng số đo bằng 90^o )

#4. Định nghĩa và tính chất của tam giác cân

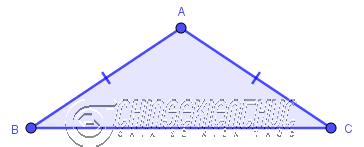
Tam giác có hai cạnh bằng nhau thì được gọi là tam giác cân.

Tam giác ABC có AB = AC nên tam giác ABC là tam giác cân (cân tại A)

Khi đó:

• AB, AC được gọi là cạnh bên
• BC được gọi là cạnh đáy

Trong một tam giác cân ta luôn có hai góc ở đáy bằng nhau:

Tam giác ABC là tam giác cân (cân tại A) nên $\hat{B}=\hat{C}$

Chú ý: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân, đây là một trong những cách giúp chúng ta chứng minh được tam giác đã cho là tam giác cân.

#5. Định nghĩa và tính chất của tam giác vuông cân

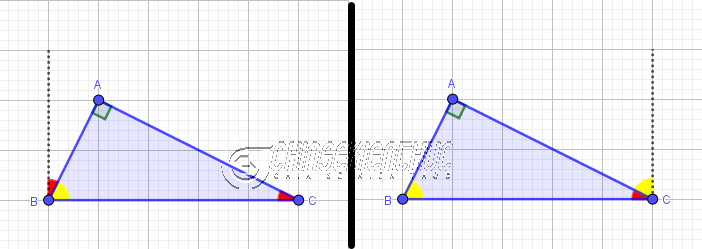
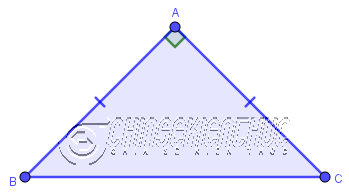
Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

Như hình trên: Tam giác vuông ABC (vuông ở A) có AB = AC => nên tam giác vuông ABC là tam giác vuông cân tại A.

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

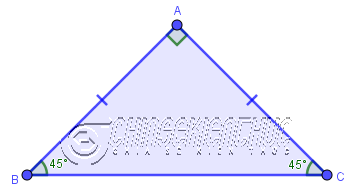
Trong một tam giác vuông cân ta luôn có hai góc ở đáy bằng 45⁰ (hay nói cách khác là hai góc nhọn bằng 45⁰)

#6. Định nghĩa và tính chất của tam giác đều

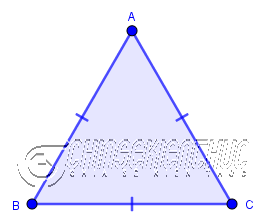
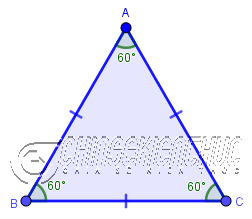
Tam giác có ba cạnh bằng nhau được gọi là tam giác đều.

Tam giác ABC có AB = BC = CA => nên tam giác ABC là một tam giác đều.

Trong một tam giác đều ta luôn có số đo của mỗi góc bằng 60⁰

#7. Lời kết

Vâng, trên đây là định nghĩa và tính chất của tam giác nhọn, tam giác tù, tam giác vuông, tam giác cân, tam giác vuông cân, tam giác đều. Đây đều là những tam giác đặc biệt !

Các bạn chú ý là khi vẽ hình học, chúng ta không được vẽ các tam giác đặc biệt, trừ khi đề bài cho các tam giác đặc biệt.

Bởi việc vẽ các tam giác đặc biệt dễ gây ra nhầm lẫn trong quá trình giải bài tập.

Ngoài ra còn một kinh nghiệm nữa là khi vẽ các tam giác thường thì bạn nên vẽ tam giác nhọn thay vì tam giác tù.

Bởi việc vẽ tam giác nhọn sẽ mang lại cho chúng ta khá nhiều lợi ích khi vẽ các đường thẳng đồng quy, đường tròn ngoại tiếp, đường tròn nội tiếp, khi cần nối dài các đường thẳng để tìm giao điểm, …

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 3 cách chứng minh hai tam giác bằng nhau (có ví dụ dễ hiểu)
• Áp dụng định lý tổng ba góc của một tam giác để giải bài tập
• 2 cách tính độ dài cạnh huyền trong tam giác vuông (rất dễ)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com