Chào các bạn, hôm trước mình đã hướng dẫn bạn cách viết phương trình đường tròn và cách viết phương trình đường thẳng trong không gian rồi.
Vậy nên hôm nay mình sẽ tiếp tục hướng dẫn cho các bạn cách viết phương trình mặt phẳng trong không gian. Cụ thể là viết phương trình mặt phẳng khi biết:
- Một điểm đi qua và một véc tơ pháp tuyến
- Ba điểm đi qua
Tương ứng với mỗi trường hợp mình sẽ bắt đầu bằng việc trình bày lý thuyết và kết thúc bằng một hoặc một vài ví dụ minh họa tương ứng:
Mục Lục Nội Dung
Trường hợp #1. Biết một điểm đi qua và một véc tơ pháp tuyến
Phương trình mặt phẳng đi qua điểm $M_0=(x_0; y_0; z_0)$ và nhận véc tơ $\vec{n}=(A; B; C)$ khác véc tơ $\vec{0}=(0; 0; 0)$ làm véc tơ pháp tuyến sẽ là $A(x-x_0)+B(y-y_0)+C(z-z_0)=0$
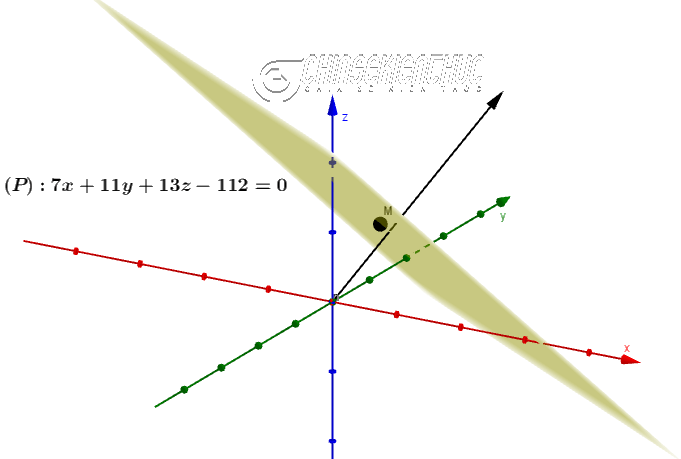
Ví dụ 1. Viết phương trình mặt phẳng $(P)$ biết mặt phẳng $(P)$ đi qua điểm $M=(2; 3; 5)$ và nhận véc tơ $\vec{n}=(7; 11; 13)$ làm véc tơ pháp tuyến
Lời giải:
Phương trình mặt phẳng $(P)$ có dạng $A(x-x_0)+B(y-y_0)+C(z-z_0)=0$
Vì $(P)$ đi qua $M=(2; 3; 5)$ và nhận véc tơ $\vec{n}=(7; 11; 13)$ làm véc tơ pháp tuyến nên phương trình của mặt phẳng $(P)$ là $7(x-2)+11(y-3)+13(z-5)=0$ hay $7x+11y+13z-112=0$
Vậy => phương trình của mặt phẳng $(P)$ là $7x+11y+13z-112=0$
Trường hợp #2. Biết ba điểm đi qua
- Cách 1. Phù hợp với học sinh Trung học Phổ thông, sinh viên Cao Đẳng và Đại học
- Cách 2. Chỉ phù hợp với sinh viên Cao Đẳng và Đại học
Các bạn lưu ý là Cách 2 không phù hợp với học sinh Trung học Phổ thông vì các bạn này chưa được học định nghĩa ma trận và tất nhiên cũng không thể tính được định thức của ma trận vuông cấp 3 x 3.
Cách 1. Dựa vào tích có hướng của hai véc tơ
Giả sử mặt phẳng $(P)$ đi qua ba điểm $A=(x_a; y_a; z_a); B=(x_b; y_b; z_b); C=(x_c; y_c; z_c)$
Lúc bấy giờ chúng ta có thể tìm phương trình của mặt phẳng $(P)$ theo các bước bên dưới:
Bước 1. Tính véc tơ $\overrightarrow{AB}=(x_b-x_a; y_b-y_a; z_b-z_a), \overrightarrow{AC}=(x_c-x_a; y_c-y_a; z_c-z_a)$
Bước 2. Tính tích của hướng của véc tơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$
Ở đây mình sẽ đặt $\overrightarrow{AB}=(x_1; y_1; z_1), \overrightarrow{AC}=(x_2; y_2; z_2)$ để thuận tiện cho việc trình bày
$[\overrightarrow{AB}; \overrightarrow{AC}]=(x_2y_3-y_2x_3; x_3y_1-y_3x_1; x_1y_2-y_1x_2)$
Công thức tính khá dài nhưng không sao vì chúng ta có thể tính được bằng máy tính CASIO fx-580VN X
Chú ý:
- Tích có hướng của hai véc tơ là một véc tơ.
- Tích có hướng của véc tơ $\vec{a}$ và $\vec{b}$ thường được kí hiệu là $[\vec{a}; \vec{b}]$ hoặc $\vec{a} \land \vec{b}$.
Lúc bấy giờ véc tơ $\vec{n}=[\overrightarrow{AB}; \overrightarrow{AC}]$ là một véc tơ pháp tuyến của mặt phẳng $(P)$
Bước 3. Viết phương trình mặt phẳng đi qua điểm A hoặc B hoặc C và nhận véc tơ $\vec{n}$ làm véc tơ pháp tuyến.
Cách 2. Dựa vào định thức của ma trận vuông cấp 3 x 3
Cho ba điểm không thẳng hàng $A=(x_a; y_a; z_a); B=(x_b; y_b; z_b); C=(x_c; y_c; z_c)$ phương trình của mặt phẳng $(P)$ đi qua ba điểm vừa cho là
$\left|\begin{array}{ccc} x-x_{a} & y-y_{a} & z-z_{a}\\ x_{b}-x_{a} & y_{b}-y_{a} & z_{b}-z_{a}\\ x_{c}-x_{a} & y_{c}-y_{a} & z_{c}-z_{a}\end{array}\right|=0$
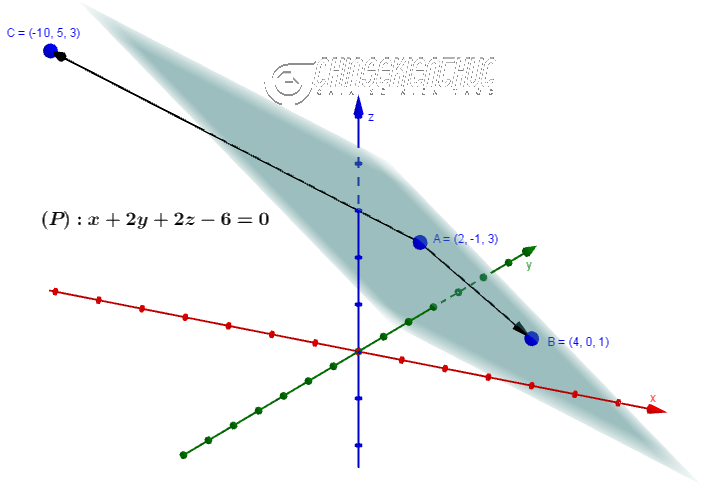
Ví dụ 2. Trong không gian $Oxyz$ cho ba điểm $A=(2; -1; 3), B=(4; 0; 1), C=(-10; 5; 3)$. Hãy viết phương trình mặt phẳng $(P)$ đi qua ba điểm vừa cho
Lời giải:
Cách 1. Dựa vào tích có hướng của hai véc tơ
$\overrightarrow{AB}=(2; 1; -2), \overrightarrow{AC}=(-12; 6; 0)$
Tích có hướng của $\overrightarrow{AB}$ và $\overrightarrow{AC}$ là $\vec{n}=[\overrightarrow{AB}; \overrightarrow{AC}]=(12; 24; 24)$
Vì $(P)$ đi qua $A=(2; -1; 3)$ và nhận véc tơ $\vec{n}=(12; 24; 24)$ làm véc tơ pháp tuyến nên phương trình của mặt phẳng $(P)$ là $12(x-2)+24(y+1)+24(z-3)=0$ hay $x+2y+2z-6=0$
Vậy => phương trình của mặt phẳng $(P)$ là $x+2y+2z-6=0$
Cách 2. Dựa vào định thức của ma trận vuông cấp 3 x 3
Phương trình mặt phẳng $(P)$ là $\left|\begin{array}{ccc} x-2 & y+1 & z-3\\ 4-2 & 0+1 & 1-3\\ -10-2 & 5+1 & 3-3\end{array}\right|=0$
$\Leftrightarrow \left|\begin{array}{ccc} x-2 & y+1 & z-3\\ 2 & 1 & -2\\ -12 & 6 & 0\end{array}\right|=0 \Leftrightarrow 12x-72+24z+24y=0 \Leftrightarrow x+2y+2z-6=0$
Vậy phương trình của mặt phẳng $(P)$ là $x+2y+2z-6=0$
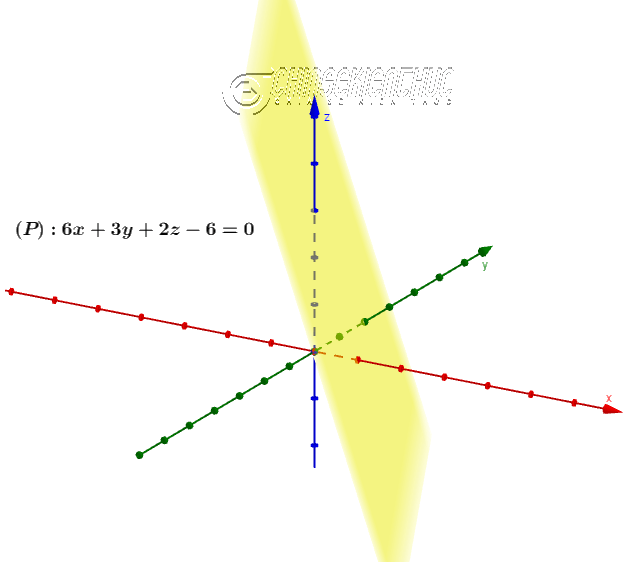
Ví dụ 3. Trong không gian $Oxyz$ cho ba điểm $A=(1; 0; 0), B=(0; 2; 0), C=(0; 0; 3)$. Hãy viết phương trình mặt phẳng $(P)$ đi qua ba điểm vừa cho
Nhận xét:
Tọa độ ba điểm mà mặt phẳng đi qua lần lượt có dạng $(a; 0; 0), (0; b; 0), (0; 0; c)$, với a, b, c là các số thực khác 0
Đây là một trường hợp đặc biệt, chúng ta nên sử dụng cách đặc biệt để tiết kiệm thời gian và công sức giải.
Cụ thể phương trình mặt phẳng đi qua ba điểm $(a; 0; 0), (0; b; 0), (0; 0; c)$ với a, b, c là các số thực khác 0 là $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
Lời giải:
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Áp dụng phương trình của mặt phẳng theo đoạn chắn ta có phương trình có mặt phẳng $(P)$ là $\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1$ hay $6x+3y+2z-6=0$
Chú ý:
Tất nhiên, bạn vẫn có thể sử dụng Cách 1 hoặc Cách 2 để tìm phương trình của mặt phẳng này bạn nhé.
Thủ thuật tính nhanh tích có hướng của hai véc tơ
Thủ thuật này khá nhiều thao tác nhưng nó không hề phức tạp, sau khi hiểu và quen tay bạn chỉ cần không tới một phút là có thể hoàn thành và tìm ra đáp án.
Ở đây mình sẽ minh họa cho $\overrightarrow{AB}=(2; 1; -2)$ và $\overrightarrow{AC}=(-12; 6; 0)$
Bước 1. Chọn phương thức tính toán Vector
Bước 2. Gán véc tơ $\overrightarrow{AB}$ vào VctA
Bước 2.1. Chọn VctA
Bước 2.2. Nhấn phím số 3
Bước 2.3. Nhập tọa độ cho véc tơ VctA
Bước 3. Gán véc tơ $\overrightarrow{AC}$ vào VctB
Bước 3.1. Nhấn phím OPTN => chọn Define Vector
Bước 3.2. Chọn VctB
Bước 3.3. Nhấn phím số 3
Bước 3.4. Nhập tọa độ cho véc tơ VctB
Bước 4. Tính tích có hướng của VctA và VctB
Bước 4.1. Nhấn phím AC => nhấn phím OPTN => nhấn phím số 3
Bước 4.2. Nhấn phím “nhân”
Bước 4.3. Nhấn phím OPTN => nhấn phím số 4
Bước 4.4. Nhấn phím =
Vậy => $[\overrightarrow{AB}; \overrightarrow{AC}]=(12; 24; 24)$
Lời kết
Vâng, trên đây là 2 trường hợp viết phương trình mặt phẳng thường gặp nhất.
Giữa Trường hợp 1 và Trường hợp 2 còn có một trường hợp trung gian nữa để viết phương trình mặt phẳng khi biết một điểm đi qua và hai véc tơ chỉ phương.
Nếu gặp trường hợp này bạn có thể quy về một trong hai trường hợp trên rồi tiến hành viết bằng cách dựa vào các kiến thức đã có.
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống