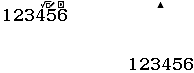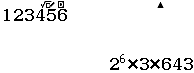Số nguyên tố là gì? hợp số là gì? Bảng các số nguyên tố

Qua bài viết này các bạn cần hiểu và phát biểu được định nghĩa về số nguyên tố, kiểm tra được một số tự nhiên bất kỳ có phải là số nguyên tố hay không và biết cách phân tích một số ra thừa số nguyên tố..

Vâng, còn tốt hơn nữa là bạn ghi nhớ được các số nguyên tố nhỏ hơn 100 và biết cách lập bảng các số nguyên tố.

I. Số nguyên tố, hợp số

#1. Số nguyên tố là gì?

Số nguyên tố là số tự nhiên lớn hơn 1 và chỉ có hai ước là 1 và chính nó.

Ví dụ: 2, 3, 5, 7, 11, 13, 17 là những số nguyên tố. Đơn giản là vì những số này chỉ chia hết cho 1 và chính nó.

#2. Số nguyên tố cùng nhau là gì?

Số nguyên tố cùng nhau là số tự nhiên có ước chung lớn nhất (UCLN) bằng 1.

Ví dụ: 2 và 5 là nguyên tố cùng nhau vì chúng có ước chung lớn nhất là 1

#3. Hợp số là gì?

Hợp số là số tự nhiên lớn hơn 1 và có nhiều hơn hai ước.

Ví dụ: 4, 6, 8, 9, 10, 12 là những hợp số.

#4. Bảng các số nguyên tố nhỏ hơn 100

2        3        5        7        11      13      17      19      23      29

31      37      41      43      47      53      59      61      67      71

73      79      83      89      97

#5. Cách chứng minh một số là số nguyên tố hoặc hợp số

Để chứng minh một số là số nguyên tố thì chúng ta phải chứng minh số đó chỉ có hai ước duy nhất là 1 và chính nó.

Trong thực hành, để chứng minh a là một số nguyên tố thì chúng ta cần chứng minh rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.

Cách kiểm tra một số có phải số nguyên tố hay không với máy tính CASIO fx-580VN X.

Giả sử chúng ta cần kiểm tra số a có phải là số nguyên tố hay không thì ta làm như sau:

• Bước 1. Gán số a vào biến nhớ x
• Bước 2. Nhập biểu thức $\frac{x}{Int(\sqrt{x})}$ => nhấn phím =

Mục đích là để tìm ra “giá trị dừng” của thuật giải.

• Bước 3. Nhấn phím x => nhấn phím =
• Bước 4. Nhập biểu thức $\frac{x}{x \div Ans + 2}$ => nhấn phím = liên tục cho đến khi nào gặp “giá trị dừng” hoặc lớn hơn “giá trị dừng” thì dừng nhấn.

Quan sát màn hình kết quả nếu từ phím = đầu tiên đến phím = cuối cùng không có kết quả nào có giá trị là một số tự nhiên thì a là số nguyên tố.

Muốn chứng minh một số là hợp số ta chỉ cần chỉ ra tồn tại ước số thứ ba (ước này khác 1 và chính nó)

#6. Có thể bạn chưa biết

II. Thừa số nguyên tố

#1. Thừa số nguyên tố là gì?

Khi chúng ta viết một số dưới dạng tích của các thừa số nguyên tố thì ta nói số đó đã được phân tích ra thành thừa số nguyên số.

$246=2.3.41$

#2. Cách phân tích một số ra thừa số nguyên tố

2.1. Phương pháp Toán học

Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố thì ta chia a lần lượt cho các số nguyên tố từ nhỏ đến lớn.

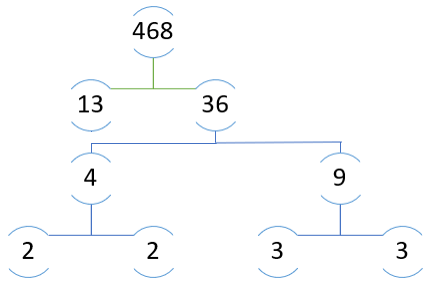
Ví dụ. Phân tích số 468 ra thừa số nguyên tố:

Vậy => $468=2.2.3.3.13=2^2.3^2.13$

Có khá nhiều cách để phân tích một số ra thừa số nguyên tố, cách mà mình vừa phân tích ở trên được gọi là phân tích theo cột dọc (cách này có tính thuật toán).

Ngoài cách trên ra thì trong SGK còn giới thiệu cho chúng ta một cách nữa mang tính trực quan hơn, gọi là phân tích theo sơ đồ cây.

#2.2. Phương pháp phân tích bằng máy tính CASIO

Giả sử chúng ta cần phân tích số 123456 ra thừa số nguyên tố:

Bước 1. Nhập số 123456 vào máy tính => nhấn phím =

Bước 2. Nhấn phím SHIFT => rồi nhấn phím

 

Vậy => $123456=2^6 \times 3 \times 643$

III. Công thức xác định các số lượng các ước của một số

Tổng quát đối với số $m=a^x \cdot b^y \cdot c^z \cdots$

Ta có ước của $m$ là số có dạng $A \cdot B \cdot C \cdots $ với:

• $A$ có $x+1$ cách chọn $a^0, a^1, a^2, \cdots, a^x$
• $B$ có $y+1$ cách chọn $b^0, b^1, b^2, \cdots, a^y$
• $C$ có $z+1$ cách chọn $c^0, c^1, c^2, \cdots, a^z$
• $\cdots$

=> Số lượng các ước của $m$ bằng $(x+1)(y+1)(z+1) \cdots$

IV. Lời kết

Vâng, như vậy là qua bài viết này bạn đã biết được số nguyên tố là gì, hợp số là gì, số nguyên tố cùng nhau là gì, bảng các số nguyên tố, cũng như cách chứng minh một số là số nguyên tố hoặc hợp số…. và khá nhiều kiến thức khác nữa.

Số nguyên tố đã được nghiên cứu từ rất xa xưa, thậm chí từ nhiều thế kỉ trước công nguyên. Tuy nhiên, cho đến nay vẫn còn nhiều bài toán liên quan đến số nguyên tố chưa tìm được lời giải.

Gôn-bach-Ơ-le là một trong những bài tiêu biểu, nếu yêu thích Số học, bạn có thể nghiên cứu thử biết đâu may mắn sẽ mỉm cười với bạn :))

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !

Đọc thêm:

• Hằng đẳng thức là gì? 7 hằng đẳng thức đáng nhớ (có ví dụ)
• Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng CASIO

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com