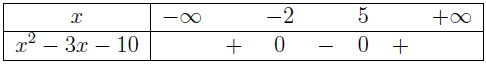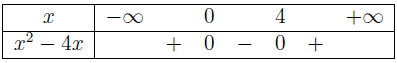Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Bất phương trình chứa ẩn trong dấu căn bậc hai nói riêng hay bất phương trình vô tỉ nói chung là một trong những bất phương trình Đại số khó giải nhất.
Muốn giải được bất phương trình này một cách nhanh chóng và chính xác thì ngoài các kiến thức được trình bày bên dưới ra thì bạn cũng nên xem lại những kiến thức sau đây:
- Cách giải bất phương trình bậc nhất một ẩn
- Cách giải bất phương trình bậc hai một ẩn
- Các tìm giao, tìm hợp, phần bù và hiệu của hai tập hợp
Mục Lục Nội Dung
#1. Bất phương trình chứa ẩn trong dấu căn bậc hai là gì?
Bất phương trình chứa ẩn trong dấu căn bậc hai là bất phương trình Đại số có dạng (hoặc có thể biến đổi để đưa về dạng) $\sqrt{f(x)}>g(x)$
$\sqrt{x^2-3 x-10}<x-2, \sqrt{x^2-4 x}>x-3$ là những bất phương trình chứa ẩn trong dấu căn bậc hai
#2. Cách giải bất phương trình chứa ẩn trong dấu căn bậc hai
Khi giải bất phương trình chứa ẩn trong dấu căn bậc hai chúng ta thường thực hiện một số phép biến đổi tương đương để chuyển nó về bất phương trình không còn chứa ẩn trong dấu căn bậc hai.
Trong quá trình biến đổi chúng ta cần:
- Nêu các điều kiện xác định của bất phương trình
- Nêu các điều kiện của nghiệm
Gộp các điều kiện đó với bất phương trình vừa nhận được chúng ta có một hệ bất phương trình tương đương với bất phương trình đã cho.
#3. Bài tập giải bất phương trình chứa ẩn trong dấu căn bậc hai
Ví dụ 1. Giải bất phương trình $\sqrt{x^2-3 x-10}<x-2$
Hướng dẫn:
Biểu thức dưới dấu căn bậc hai phải không âm => $x^2-3 x-10 \geq 0$
Suy ra điều kiện xác định của bất phương trình đã cho là $x^2-3 x-10 \geq 0$ $(1)$
Đặt $f(x)=x^2-3 x-10$
Vì $a=1>0$ và $f(x)$ có hai nghiệm $x_1=-2$, $x_2=5$ nên chúng ta có bảng xét dấu $f(x)$
Vậy điều kiện xác định của bất phương trình đã cho là $x \leq -2, x \geq 5$
Biểu thức căn bậc hai phải không âm và dấu của bất phương trình là dấu bé hơn suy ra $x-2>0$
Suy ra nghiệm của bất phương trình đã cho phải thoả mãn điều kiện $x-2>0$ $(2)$
Vậy tập nghiệm của bất phương trình đã cho phải thỏa mãn $x>2$
Kết hợp điều kiện $(1)$ và $(2)$ với nhau => bất phương trình đã cho tương đương với bất phương trình $x^2-3 x-10<(x-2)^2$ $\Leftrightarrow$ $x-14<0$ $\Leftrightarrow$ $x<14$ $(3)$
Vậy bất phương trình đã cho tương đương với hệ gồm ba bất phương trình $(1)$, $(2)$ và $(3)$
$\left\{\begin{array}{l} \left[\begin{array}{l}x \leq -2 \\ x \geq 5 \end{array}\right. \\ x>2 \\ x<14 \end{array}\right.$
Vậy => tập nghiệm của bất phương trình đã cho là $[5, 14)$
Lời giải:
$\sqrt{x^2-3 x-10}<x-2$ $(*)$
$(*) \Leftrightarrow \left\{\begin{array}{l} x^2-3 x-10 \geq 0 \\ x-2>0 \\ x^2-3 x-10<(x-2)^2 \end{array}\right.$
$(*) \Leftrightarrow \left\{\begin{array}{l} \left[\begin{array}{l}x \leq -2 \\ x \geq 5 \end{array}\right. \\ x>2 \\ x<14 \end{array}\right.$
$(*) \Leftrightarrow 5\leq x < 14$
Vậy tập nghiệm của bất phương trình đã cho là $[5, 14)$
Ví dụ 2. Giải bất phương trình $\sqrt{x^2-4 x}>x-3$
Hướng dẫn:
Biểu thức dưới dấu căn bậc hai phải không âm => $x^2-4 x \geq 0$
Suy ra điều kiện xác định của bất phương trình đã cho là $x^2-4 x \geq 0$ $(1)$
Đặt $f(x)=x^2-4 x$
Vì $a=1>0$ và $f(x)$ có hai nghiệm $x_1=0$, $x_2=4$ nên chúng ta có bảng xét dấu $f(x)$
Vậy điều kiện xác định của bất phương trình đã cho là $x \leq 0, x \geq 4$
Để khử dấu căn bậc hai chúng ta xét hai trường hợp
Trường hợp 1. $x-3<0 \Leftrightarrow x<3$ $(2)$
Dễ thấy nghiệm chung của $(1)$ và $(2)$ chính là nghiệm của bất phương trình đã cho
Nói một cách khác trong Trường hợp 1 bất phương trình đã cho tương đương với hệ gồm hai bất phương trình $(1)$ và $(2)$
$\left\{\begin{array}{l} x^2-4 x \geq 0 \\ x-3<0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l} \left[\begin{array}{l} x \leq 0 \\ x \geq 4 \end{array}\right. \\ x<3 \end{array}\right. \Leftrightarrow x \leq 0$
Trường hợp 2. $x-3 \geq 0 \Leftrightarrow x \geq 3$ $(3)$
Với các điều kiện $(1)$ và $(3)$ bất phương trình đã cho tương đương với bất phương trình $x^2-4 x>(x-3)^2 \Leftrightarrow 2x-9>0 \Leftrightarrow x>\frac{9}{2}$ $(4)$
Vì $(4)$ kéo theo $(1)$ nên nghiệm chung của hai bất phương trình $(3)$ và $(4)$ là nghiệm của bất phương trình đã cho
Nói cách khác trong Trường hợp 2 bất phương trình đã cho tương đương với hệ gồm hai bất phương trình $(3)$ và $(4)$
$\left\{\begin{array}{l} x-3 \geq 0 \\ x^2-4 x>(x-3)^2 \end{array}\right. \Leftrightarrow\left\{\begin{array}{l} x \geq 3 \\ x>\frac{9}{2} \end{array} \Leftrightarrow \quad x>\frac{9}{2}\right.$
Vậy tập nghiệm của bất phương trình đã cho là $(-\infty ; 0] \cup \left(\frac{9}{2} ;+\infty\right)$
Lời giải:
$\sqrt{x^2-4 x}>x-3$ $(*)$
$(*) \Leftrightarrow \left[\begin{array}{l} \left\{\begin{array}{l} x^2-4 x \geq 0 \\ x-3<0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l} \left[\begin{array}{l} x \leq 0 \\ x \geq 4 \end{array}\right. \\ x<3 \end{array}\right. \Leftrightarrow x \leq 0 \\ \left\{\begin{array}{l} x-3 \geq 0 \\ x^2-4 x>(x-3)^2 \end{array}\right. \Leftrightarrow \left\{\begin{array}{l} x \geq 3 \\ x>\frac{9}{2} \end{array} \Leftrightarrow \quad x>\frac{9}{2}\right.\end{array}\right. \Leftrightarrow \left[\begin{array}{l}x \leq 0 \\ x > \frac{9}{2}\end{array}\right.$
#4. Lời kết
Khi giải bất phương trình chứa ẩn trong dấu căn bậc hai các bạn cần thận trọng với các điều kiện xác định của bất phương trình và điều kiện xác định của tập nghiệm khi nào giao, khi nào hợp.
- Suy ra hệ bất phương tương đương với bất phương trình đã cho là giao.
- Vậy tập nghiệm của bất phương trình đã cho là hợp.
Ngoài ra, bạn cũng cần thận trọng không bỏ xót nghiệm khi dấu của bất phương trình là lớn hơn hoặc bằng, nhỏ hơn hoặc bằng.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Hi vọng những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
