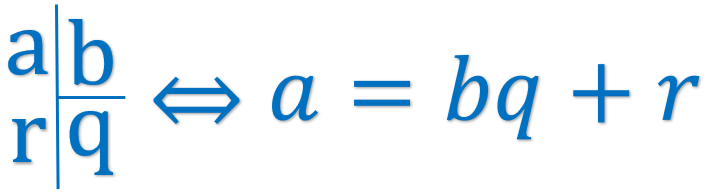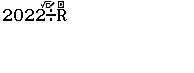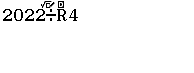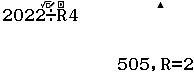Hiểu rõ hơn về Phép trừ và Phép chia các số tự nhiên

Tiếp tục mạch kiến thức, hôm nay mình và các bạn sẽ cùng nhau tìm hiểu về phép trừ và phép chia các số tự nhiên ha.

Thông qua bài viết này mà chúng ta sẽ biết khi nào hiệu hoặc thương của phép trừ hoặc phép chia là một số tự nhiên, mối quan hệ giữa các “số” trong phép trừ, phép chia hết và phép chia có dư.

I. Phép trừ các số tự nhiên

Khi lấy số tự nhiên a trừ cho số tự nhiên b chúng ta sẽ thu được số tự nhiên c

$a-b=c$, a được gọi là số bị trừ, b là số trừ, còn c là hiệu.

Ở đây chúng ta đang nói đến phép trừ hai số tự nhiên nên điều kiện để có thể thực hiện được phép trừ là $a \geq b$

Mối quan hệ của số bị trừ, số trừ, hiệu và phép cộng được thể hiện bởi biểu thức số trừ cộng với hiệu bằng số bị trừ

Mối quan hệ này rất thường gặp trong cuộc sống hằng ngày, dưới đây là một ví dụ minh họa tiêu biểu:

Ông Minh đi chợ Bến Tre mua dưa leo hết 26.000, ông đưa cho người bán tờ 100.000. Người bán thối lại 4.000 và nói 30.000, đưa tiếp 20.000 và nói 50.000, rồi đưa tiếp 50.000 và nói đủ 100.000. Nhiều người có thói quen trả từng tờ vậy đó 🙂

II. Phép chia các số tự nhiên

Thật ra phép chia hết là trường hợp đặc biệt của phép chia có dư nhưng vì lý do sư phạm nên mình quyết định trình bày thành hai trường hợp.

#1. Phép chia hết

Cho hai số tự nhiên a và b (b khác 0) nếu tồn tại số tự nhiên x sao cho $bx=a$ thì ta nói a chia hết cho b

$a:b=x$ a được gọi là số bị chia, b là số chia và x là thương.

2022 chia hết cho 2 vì $2.1011=2022$

#2. Phép chia có dư

Cho hai số tự nhiên a và b (b khác 0), chúng ta luôn luôn tìm được hai số tự nhiên q và r (duy nhất) sao cho $a=bq+r$ với $0 \leq r < b$

a được gọi là số bị chia, b là số chia, q là thương và r là số dư.

Ví dụ. $2022=505.4+2$, 2022 là số bị chia, 4 là số chia, 505 là thương và 2 là số dư.

#3. Biểu diễn một số tự nhiên dưới dạng một biểu thức của phép chia có dư

Chúng ta có thể biểu diễn một số tự nhiên a bất kỳ dưới dạng một biểu thức của phép chia có dư. Ứng dụng này rất thường được sử dụng khi cần chứng minh các bài toán chia hết.

$a=2k+r, k \in N, r \in \{0,1\}$

$a=3k+r, k \in N, r \in \{0, 1, 2\}$

$a=5k+r, k \in N, r \in \{0, 1, 2, 3, 4\}$

#4. Thực hiện phép chia có dư bằng máy tính CASIO fx-580VN X

Tính năng $\div R$ trong máy tính CASIO fx-580VN X cho phép chúng ta thực hiện phép chia có dư một cách chính xác và nhanh chóng

Các bước thực hiện:

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Đầu tiên bạn chọn phương thức tính toán Calculate

Bước 1. Nhập số bị chia

Bước 2. Nhấn phím ALPHA rồi nhấn phím

Bước 3. Nhập số chia

Bước 4. Nhấn phím =

Vậy => 2022 chia 4 được 505 và dư 2

III. Lời kết

Dễ thấy phép tính trừ và phép tính chia là phép tính ngược của phép cộng và phép nhân

Trong thức tế của cuộc sống, người ta thường tìm cách chuyển từ phép trừ và phép chia thành phép cộng và phép nhân để việc tính toán được nhanh chóng và chính xác hơn, dễ tính nhẩm hơn.

Okay, hi vọng là những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé 🙂

• Các tính chất của phép chia hết (kí hiệu, cách áp dụng..)
• Hằng đẳng thức là gì? 7 hằng đẳng thức đáng nhớ (có ví dụ)
• 2 cách tìm BỘI CHUNG và BỘI CHUNG NHỎ NHẤT (rất dễ)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com