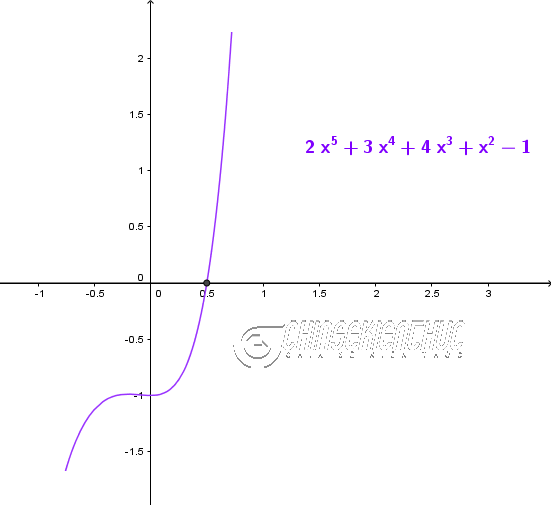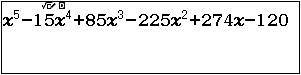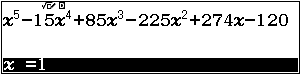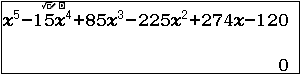Cách giải phương trình bậc năm, có nhiều ví dụ

Vâng, nói về phương trình bậc năm và các bậc lớn hơn năm là cả một câu chuyện dài, tốn không biết bao nhiêu thời gian và công sức nghiên cứu của các nhà Toán học trên thế giới.

Abel đã chứng minh được không có cách giải tổng quát cho phương trình bậc năm và lớn hơn năm.

Galois đã chỉ ra các dấu hiệu nhận biết một phương trình Đại số có thể giải được bằng căn thức hay không?

Vậy nên suy ra, với đại đa số chúng ta thì việc giải phương trình bậc năm trở lên là không khả quan, nếu có thì cũng chỉ là giải được một số lớp phương trình ở dạng đặc biệt mà thôi.

Hơn nữa, trên thực tế thì chúng ta cũng rất ít gặp phương trình có bậc năm trở lên.

Tóm lại là ở trong bài viết này mình chỉ hướng dẫn các bạn giải một số lớp phương trình bậc năm có dạng đặc biệt mà thôi ha.

#1. Phương trình bậc năm có dạng như thế nào?

Phương trình $ax^5+bx^4+cx^3+dx^2+ex+f=0$ với $a, b, c, d, e, f$ là những số thực bất kỳ và $a$ khác $0$ được gọi là phương trình bậc năm.

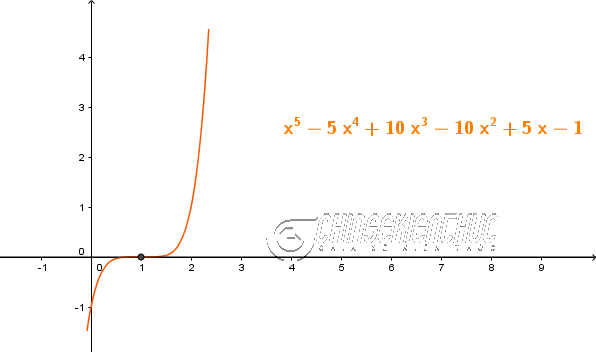
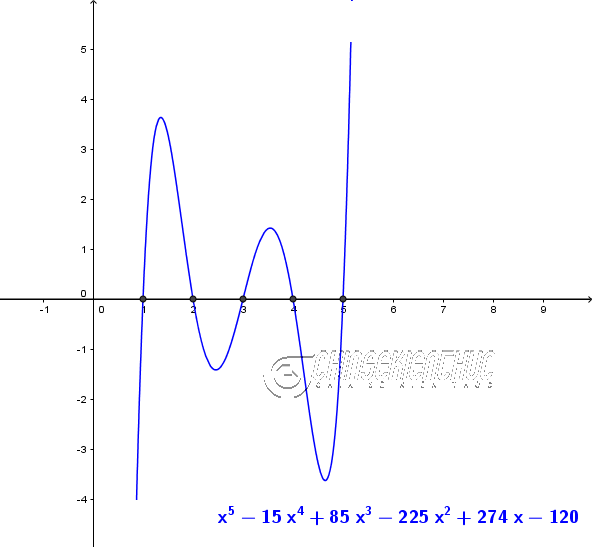
Ví dụ. $x^5-5x^4+10x^3-10x^2+5x–1=0$, $x^5-15x^4+85x^3-225x^2+274x-120=0$, $2x^5+3x^4+4x^3+x^2-1=0$ là những phương trình bậc năm

#2. Một số kiến thức cơ bản về nghiệm của phương trình bậc năm

1. Nếu $a+b+c+d+e+f=0$ thì phương trình có nghiệm là $1$
2. Nếu $a-b+c-d+e-f=0$ thì phương trình có nghiệm là $-1$
3. Nếu phương trình có nghiệm nguyên thì chỉ có thể là một trong các ước của $f$
4. Nếu phương trình có nghiệm hữu tỉ $\frac{p}{q}$ thì $p$ là các ước của $f$ và $q$ là các ước của $a$
5. Phương trình bậc năm có không quá năm nghiệm.

Trong thực hành, chúng ta sẽ hy vọng và lần lượt kiểm tra phương trình bậc năm đã cho có rơi vào một trong bốn dạng đặc biệt trên không, nếu có chúng ta sẽ giải được một cách dễ dàng.

#3. Bài tập ví dụ

Ví dụ 1. Giải phương trình $x^5-5x^4+10x^3-10x^2+5x–1=0$

Cách 1. Dựa vào hệ quả của định lý Viét

Dễ thấy, $1+(-5)+10+(-10)+5+(-1)=0$ suy ra phương trình có nghiệm là $1$

Suy ra $x^5-5x^4+10x^3-10x^2+5x–1=0 \Leftrightarrow (x-1)(x^4-4x^3+6x^2-4x+1)=0$

Phương trình $x^4-4x^3+6x^2-4x+1=0$ là một phương trình bậc bốn nên chắc chắn có thể giải được

$x^4-4x^3+6x^2-4x+1=0$ $(*)$

$(*) \Leftrightarrow (x-1)(x^3-3x^2+3x-1)=0 \Leftrightarrow (x-1)(x-1)(x^2-2x+1)=0 \Leftrightarrow (x-1)(x-1)(x-1)(x-1)=0$

Vậy tập nghiệm của phương trình đã cho là $\{1\}$

Cách 2. Dựa vào tam giác Pascal

Nếu để ý các bạn sẽ thấy, các hệ số của phương trình lần lượt là các mảng số của tam giác Pascal (dòng thứ sáu).

Suy ra $x^5-5x^4+10x^3-10x^2+5x–1=0 \Leftrightarrow (x-1)^5=0 \Leftrightarrow x-1=0 \Leftrightarrow x=1$

Vậy tập nghiệm của phương trình đã cho là $\{1\}$

Ví dụ 2. Giải phương trình $x^5-15x^4+85x^3-225x^2+274x-120=0$

Cách 1. Dựa vào hệ quả của định lý Viét

Dễ thấy $1+(-15)+85+(-225)+274+(-120)=0$ => phương trình có nghiệm là $1$

Suy ra $x^5-15x^4+85x^3-225x^2+274x-120=0 \Leftrightarrow (x-1)(x^4-14x^3+71x^2-154x+120)=0$ $(*)$

Phương trình $x^4-14x^3+71x^2-154x+120=0$ là một phương trình bậc bốn nên chắc chắn có thể giải được, phương trình này có rất nhiều cách giải, ở đây mình sẽ phân tích để chuyển về việc giải phương trình bậc hai

$(*) \Leftrightarrow (x^2-7x)^2+22(x^2-7x)+120=0$ $(**)$

Đặt $t=x^2-7x$

Phương trình $(**)$ trở thành $t^2+22t+120=0 \Leftrightarrow \left[\begin{array}{l} t=-10\\ t=-12\end{array}\right.$

• Với $t=-10$ ta được phương trình $-10=x^2-7x \Leftrightarrow x^2-7x+10=0 \Leftrightarrow \left[\begin{array}{l} x=5\\ x=2\end{array}\right.$
• Với $t=-12$ ta được phương trình $-12=x^2-7x \Leftrightarrow x^2-7x+12=0 \Leftrightarrow \left[\begin{array}{l} x=4\\ x=3\end{array}\right.$

Vậy tập nghiệm của phương trình đã cho là $\{1, 2, 3, 4, 5\}$

Cách 2. Tìm nghiệm nguyên, nghiệm hữu tỉ

Truy cập vào trang web: https://www.wolframalpha.com/

Dễ thấy $\pm 1, \pm 2, \pm 3, \pm 4, \pm 5 ,\pm 6, \pm 8, \pm 10, \pm 12, \pm 15, \pm 20, \pm 24, \pm 30, \pm 40, \pm 60, \pm 120$ là các ước của $-120$

Lần lượt thay các ước của $-120$ vào vế trái của phương trình, ước nào làm cho vế trái bằng $0$ thì đó chính là nghiệm

$(1)^5-15(1)^4+85(1)^3-225(1)^2+274(1)-120=0$

$(2)^5-15(2)^4+85(2)^3-225(2)^2+274(2)-120=0$

$(3)^5-15(3)^4+85(3)^3-225(3)^2+274(3)-120=0$

$(4)^5-15(4)^4+85(4)^3-225(4)^2+274(4)-120=0$

$(5)^5-15(5)^4+85(5)^3-225(5)^2+274(5)-120=0$

Thật may mắn, chỉ sau 5 lần thử chúng ta đã tìm đủ năm nghiệm của phương trình, không cần thử các giá trị còn lại vì phương trình bậc năm có không quá năm nghiệm mà 🙂

Vậy => tập nghiệm của phương trình đã cho là $\{1, 2, 3, 4, 5\}$

Ví dụ 3. Giải phương trình $2x^5+3x^4+4x^3+x^2-1=0$

Dễ thấy $\pm 1$ không là nghiệm của phương trình.

Ở đây chúng ta sẽ hy vọng phương trình có nghiệm hữu tỉ để có thể giải được một cách dễ dàng.

• $-1$ có hai ước là $\pm 1$
• $2$ có bốn ước là $\pm 2, \pm 1$

Suy ra phương trình đã cho nếu có nghiệm hữu tỉ thì chỉ có thể là một trong các giá trị $\frac{1}{2}, -\frac{1}{2}, 1, -1$

Lần lượt thay các giá trị vừa tìm được vào vế trái của phương trình, giá trị nào làm cho vế trái bằng 0 thì đó chính là nghiệm

• $2\left(\frac{1}{2}\right)^5+3\left(\frac{1}{2}\right)^4+4\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^2-1=0$
• $2\left(-\frac{1}{2}\right)^5+3\left(-\frac{1}{2}\right)^4+4\left(-\frac{1}{2}\right)^3+\left(-\frac{1}{2}\right)^2-1=-\frac{9}{8}$
• $2(1)^5+3(1)^4+4(1)^3+(1)^2-1=9$
• $2(-1)^5+3(-1)^4+4(-1)^3+(-1)^2-1=-3$

Suy ra $\frac{1}{2}$ là nghiệm của phương trình

Suy ra $2x^5+3x^4+4x^3+x^2-1=0 \Leftrightarrow \left(x-\frac{1}{2}\right)(x^4+2x^3+3x^2+2x+1)=0 \Leftrightarrow \left(x-\frac{1}{2}\right)(x^2+x+1)^2=0$

Vì $(x^2+x+1)=\left(x+\frac{1}{2}\right)^2+\frac{3}{4} > 0$ nên $(x^2+x+1)^2 > 0$

Vậy => tập nghiệm của phương trình đã cho là $\left\{\frac{1}{2}\right\}$

#4. Thử nhanh các giá trị bằng máy tính CASIO

Bước 1. Nhập vế trái của phương trình vào máy tính.

Bước 2. Sau đó lần lượt nhấn các phím  để thử với ước $1$

Bước 3. Lập lại Bước 2 với các ước còn lại.

Lần lượt nhấn các phím  để thử với ước $2$

…

#5. Lời kết

Trong thực tế, hầu hết các trường hợp chúng ta sẽ gặp các phương trình bậc năm có dạng đặc biệt.

Lúc này bạn chỉ cần cố gắng tìm ra điểm đặc biệt của nó là có thể giải được (nên dựa vào các kiến thức mà mình đã cung cấp).

Sau khi tìm được một nghiệm thì chúng ta sẽ phân tích thành phương trình tích với nhân tử đầu tiên là nhị thức, nhân tử thứ hai là một phương trình bậc bốn.

Phương trình bậc bốn có nhiều cách giải hơn phương trình bậc năm và hơn hết là có cách giải tổng quát.

Trường hợp không may nếu gặp phương trình không có gì đặc biệt thì bạn có thể sử dụng máy tính CASIO để dò tìm trước một nghiệm bất kỳ.

Sau đó từ nghiệm tìm được thì chúng ta sẽ cố gắng phân tích, chuyển phương trình đã cho về phương trình tích để giải.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn