Định lý Talet là một trong những định lý lâu đời nhất, được ứng dụng nhiều nhất trong Toán học, cũng như trong thực tiễn của cuộc sống của chúng ta.
Định lý Talet ngoài việc giúp chúng ta tính được độ dài của những đoạn thẳng tương ứng tỉ lệ, chứng minh được hai đường thẳng song song.. thì nó còn giúp chúng ta chứng minh được:
- Hai tam giác đồng dạng
- Định lý Menelaus
- Định lý Routh…
Mục Lục Nội Dung
#1. Định lý Talet trong tam giác
Chúng ta đọc là định lý Ta-lét (Thales) <được đặt theo tên nhà toán học người Hy Lạp Thales> !
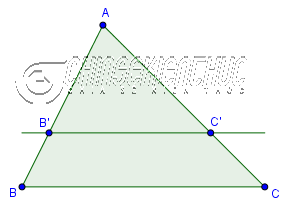
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
| Giả thuyết | $\triangle ABC, B’C’ \parallel BC (B’ \in AB, C’ \in AC)$ |
| Kết luận | $\frac{AB’}{AB}=\frac{AC’}{AC}, \frac{AB’}{B’B}=\frac{AC’}{C’C}, \frac{B’B}{AB}=\frac{C’C}{AC}$ |
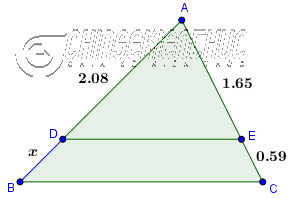
Ví dụ 1. Cho tam giác ABC, trên AB lấy điểm D sao cho DA = 2.08, qua D kẻ đường thẳng song song với BC cắt AC tại E
Tính độ dài đoạn thẳng DB, biết AE=1.65, EC=0.59
Lời giải:
Vì DE song song với BC, áp dụng định lí Talet vào tam giác ABC ta được $\frac{AD}{DB}=\frac{AE}{EC} \Leftrightarrow \frac{2.08}{DB}=\frac{1.65}{0.59}$
Suy ra $DB=\frac{2.08 \times 0.59}{1.65}=\frac{3068}{4125} \approx 0.74$
Vậy độ dài đoạn thẳng DB gần bằng 0.74 ĐVĐD
#2. Phát biểu định lý Talet đảo
Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với hai cạnh còn lại của tam giác.
| Giả thuyết | $\triangle ABC, B’ \in AB, C’ \in AC, \frac{AB’}{B’B}=\frac{AC’}{C’C}$ |
| Kết luận | $B’C’ \parallel BC$ |
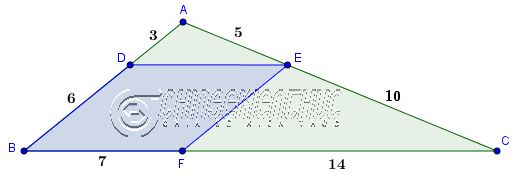
Ví dụ 2. Cho tam giác ABC có AB=9, AC=15, BC=21. Trên cạnh AB lấy điểm D sao cho AD=3, cạnh AC lấy điểm E sao cho AE=5, cạnh BC lấy điểm F sao cho EF=7
Chứng minh tứ giác DEFB là hình bình hành.
Lời giải:
$\frac{AD}{DB}=\frac{3}{6}=\frac{1}{2}$ và $\frac{AE}{EC}=\frac{5}{10}=\frac{1}{2}$
Suy ra $\frac{AD}{DB}=\frac{AE}{EC}$
Theo định lý Talet đảo DE song song BF (1)
$\frac{CE}{EA}=\frac{10}{5}=2$ và $\frac{CF}{FB}=\frac{14}{7}=2$
Suy ra $\frac{CE}{EA}=\frac{CF}{FB}$
Theo định lý Talet đảo EF song song DB (2)
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Từ (1) và (2) => tứ giác DEFB là hình bình hành.
#3. Hệ quả của định lý Talet trong tam giác
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
| Giả thuyết | $\triangle ABC, B’C’ \parallel BC (B’ \in AB, C’ \in AC)$ |
| Kết luận | $\frac{AB’}{AB}=\frac{AC’}{AC}=\frac{BC’}{BC}$ |
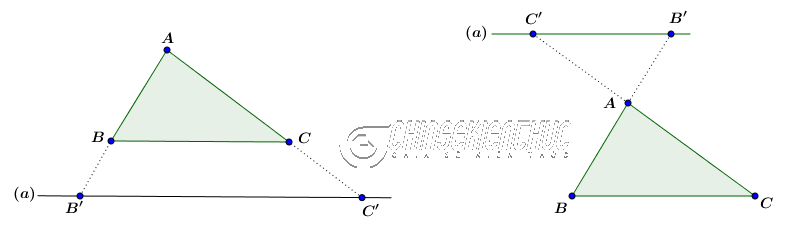
Hệ quả trên vẫn đúng cho trường hợp đường thẳng (a) song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.
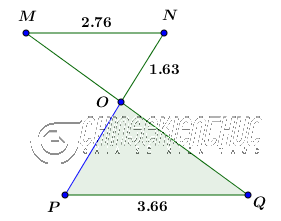
Ví dụ 3. Cho tam giác OPQ có PQ=3.66, trên tia đối của tia OP lấy điểm N sao cho ON=1.63, qua N kẻ đường thẳng (a) song song với PQ, trên đường thẳng (a) lấy điểm M sao cho MN=2.76
Tính độ dài đoạn thẳng OP.
Lời giải:
Vì MN song song PQ nên theo hệ quả của định lí Talet ta có
$\frac{NO}{OP}=\frac{MO}{OQ}=\frac{MN}{PQ}$ hay $\frac{1.63}{OP}=\frac{2.76}{3.66}$
Suy ra $OP=\frac{1.63 \times 3.66}{2.76}=\frac{9943}{4600} \approx 2.16$
Vậy => độ dài đoạn thẳng OP gần bằng 2.16
#4. Lời kết
Nhờ vào việc phát biểu định lý Talte, phát biểu hệ quả định lý Talet và cách áp dụng định lý Talet vào giải các bài tập (như ví dụ minh họa bên trên) mà chúng ta đã có cái nhìn khá toàn diện về định lý Talet trong tam giác rồi phải không nào.
Xa hơn nữa, nếu muốn nâng cao kiến thì thức bạn có thể tìm hiểu thêm định lý Talet trong hình thang. Việc làm này không có gì khó khăn cả vì định lý Talet trong hình thang chính là trường hợp mở rộng của định lý đường trung bình của hình thang.
Hi vọng là bài viết này sẽ hữu ích với bạn, xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- Định lý Pytago thuận, định lý Pytago đảo và bài tập ví dụ !
- Định nghĩa và định lý của tứ giác nội tiếp đường tròn
- Áp dụng định lý tổng ba góc của một tam giác để giải bài tập
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống