Cách giải phương trình nhiều ẩn (có nhiều ví dụ)

Xin chào tất cả các bạn !

Phương trình có từ hai ẩn trở lên thì được gọi là phương trình nhiều ẩn.

Tương tự như phương trình một ẩn, phương trình nhiều ẩn cũng có thể có một nghiệm hoặc có vô số nghiệm hoặc không có nghiệm nào (vô nghiệm).

Trong phạm vi ngắn gọn của bài viết này chúng ta sẽ cùng tìm hiểu về một lớp phương trình hai ẩn thường gặp.

Cụ thể là trong các kì thi học sinh giỏi hoặc khi giải phương trình nghiệm nguyên.

#1. Phương trình nhiều ẩn là gì?

Phương trình dạng $f(x)=0$ với $f(x)$ là biểu thức Toán học có từ hai ẩn trở lên được gọi là phương trình nhiều ẩn.

Ví dụ $x^2+2xy+y^2=3$, $x+y+x+xyz=0$ là những phương trình nhiều ẩn.

Lớp phương trình nhiều ẩn được hướng dẫn trong bài viết này là lớp phương trình hai ẩn và có thể biến đổi sơ cấp đưa về dạng $f(x)^2+g(x)^2=0$

#2. Các giải phương trình nhiều ẩn

Cho phương trình hai ẩn có dạng $ax^2+cy^2+bx+dy+f=0$

Đặt $P(x)=ax^2+cy^2+bx+dy+f$

Tiến hành biến đổi sơ cấp chúng ta được:

Bước 1. $P(x)$ $=a\left(x+\frac{1}{2}\frac{b}{a}\right)^2$ $+cy^2$ $+dy$ $+f$ $-\frac{1}{4}\frac{b^2}{a}$

Bước 2. $P(x)$ $=a\left(x+\frac{1}{2}\frac{b}{a}\right)^2$ $+c\left(y+\frac{1}{2}\frac{d}{c}\right)^2$ $+f$ $-\frac{1}{4}\frac{b^2}{a}$ $-\frac{1}{4}\frac{d^2}{c}$

Nếu $f$ $-\frac{1}{4}\frac{b^2}{a}$ $-\frac{1}{4}\frac{d^2}{c}=0$ thì phương trình $ax^2+cy^2+bx+dy+f=0$ sẽ có dạng $f(x)^2+g(x)^2=0$

Lúc này phương trình đã cho sẽ tương đương với $f(x)^2+g(x)^2=0 \Leftrightarrow \left \{\begin{array}{l} f(x)=0 \\ g(x)=0 \end{array}\right.$

#3. Cách giải phương trình nhiều ẩn

Ví dụ 1. Giải phương trình $2x^2+\frac{1}{2} y^2-2 x+y+1=0$

Cách 1.

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}+\frac{1}{2} y^2+y =0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}(y+1)^2=0$

$\Leftrightarrow \left \{ \begin{array}{l}2\left(x-\frac{1}{2}\right)^2=0 \\ \frac{1}{2}(y+1)^2=0\end{array}\right.$

$\Leftrightarrow \left \{ \begin{array}{l}x=\frac{1}{2} \\ y=-1\end{array}\right.$

Vậy phương trình đã cho có một nghiệm duy nhất là $\left(\frac{1}{2}, -1\right)$

Cách 2.

$\Leftrightarrow 2x^2-2x+\frac{1}{2}y^2+y+1=0$

$\Leftrightarrow 2\left(x^2-x\right)+\frac{1}{2}y^2+y+1=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2-\frac{1}{2}+\frac{1}{2}y^2+y+1=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}y^2+y+\frac{1}{2}=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}\left(y^2+2y\right)+\frac{1}{2}=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}\left(y+1\right)^2-\frac{1}{2}+\frac{1}{2}=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}\left(y+1\right)^2=0$

$\Leftrightarrow \left \{ \begin{array}{l}2\left(x-\frac{1}{2}\right)^2=0 \\ \frac{1}{2}(y+1)^2=0\end{array}\right.$

$\Leftrightarrow \left \{ \begin{array}{l}x=\frac{1}{2} \\ y=-1\end{array}\right.$

Vậy phương trình đã cho có một nghiệm duy nhất là $\left(\frac{1}{2}, -1\right)$

Ví dụ 2. Giải phương trình $2 x^2+8 y^2-2 x+4 y+1=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+8 y^2+4 y+\frac{1}{2}=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+8\left(y+\frac{1}{4}\right)^2=0$

$\Leftrightarrow \left \{ \begin{array}{l}2\left(x-\frac{1}{2}\right)^2=0 \\ 8(y+\frac{1}{4})^2=0\end{array}\right.$

$\Leftrightarrow \left \{ \begin{array}{l}x=\frac{1}{2} \\ y=-\frac{1}{4}\end{array}\right.$

Vậy phương trình đã cho có một nghiệm duy nhất là $\left(\frac{1}{2}, -\frac{1}{4}\right)$

Ví dụ 3. Giải phương trình $2 x^2+8 y^2-2 x+4 y+10=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+8 y^2+4 y+\frac{19}{2}=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+8\left(y+\frac{1}{4}\right)^2+9=0$

$\Leftrightarrow 2\left(x-\frac{1}{2}\right)^2+8\left(y+\frac{1}{4}\right)^2=-9$

Vậy phương trình đã cho vô nghiệm

#4. Mẹo giải phương trình nhiều ẩn bằng công cụ trực tuyến

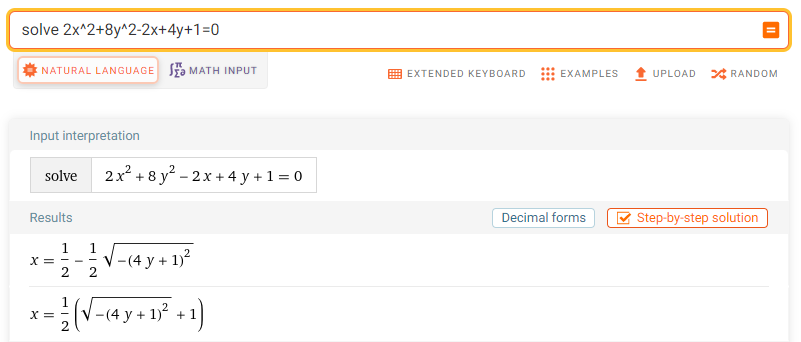
Để giải các phương trình một ẩn chúng ta thường sẽ nhập lệnh solve <phương trình>

Tuy nhiên, với các phương trình nhiều ẩn thì lệnh solve <phương trình> không cho ra kết quả mong muốn. Thật vậy !

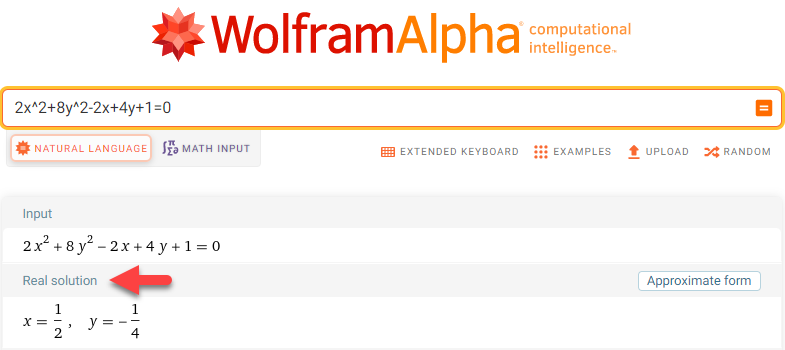
Nguyên nhân thì mình cũng không rõ nhưng giải pháp thì đã có, bạn hãy nhập phương trình vào => sau đó cuộn trang tìm đến Real solution, giá trị tại phần Real solution chính là nghiệm của phương trình đã cho.

Các bước thực hiện:

Bước 1. Truy cập vào công cụ trực tuyến Wolfram Alpha bằng cách nháy chuột vào liên kết bên dưới:

https://www.wolframalpha.com/

Bước 2. Nhập phương trình $2x^2+8y^2-2x+4y+1=0$

Bước 3. Nhấn phím Enter để xem kết quả.

#5. Lời kết

Okay, trên đây là cách giải phương trình nhiều ẩn mà mình muốn giới thiệu đến các bạn.

Bằng cách phát hiện ra các hằng đẳng thức có mặt ở vế trái của phương trình nhiều ẩn $ax^2+cy^2+bx+dy+f=0$ mà chúng ta đã giải được một cách khá dễ dàng và nhanh chóng.

Đối với lớp phương trình hai ẩn có dạng $ax^2+cy^2+bx+dy+f=0$ thì đây là cách tối ưu nhất.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 3 cách giải phương trình bậc ba (có ví dụ dễ hiểu)
• Hướng dẫn cách giải phương trình bậc năm
• 2 cách giải phương trình bậc bốn và bài tập ví dụ
• Cách giải phương trình lượng giác (có nhiều ví dụ)
• 3 cách giải phương trình chứa dấu giá trị tuyệt đối
• 7 cách giải phương trình bậc hai đơn giản, hiệu quả
• 3 cách giải phương trình trùng phương (có ví dụ dễ hiểu)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn