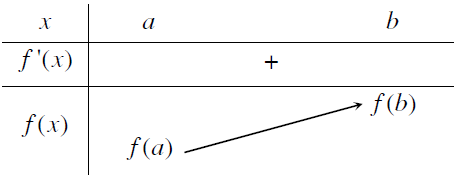Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Hôm nay, chúng ta sẽ ứng dụng các công thức tính đạo hàm và cách tính giới hạn để xét tính đơn điệu của hàm số.
Tính đơn điệu hay còn được gọi là tính đồng biến và nghịch biến của hàm số.
Tính đơn điệu là một trong các tính chất quan trọng nhất của hàm số, không thể bỏ qua kiến thức này khi khảo sát sự biến thiên của hàm số.
Mục Lục Nội Dung
#1. Điều kiện đủ để hàm số đơn điệu trên một khoảng
Trước khi tìm hiểu các bước xét tính đơn điệu của hàm số thì chúng ta cần biết điều kiện đủ để hàm số đơn điệu trên một khoảng.
Giả sử, hàm số $f(x)$ có đạo hàm trên khoảng $I$, lúc này:
- Nếu $f^{\prime}(x)>0$ với mọi $x \in I$ thì hàm số $f(x)$ đồng biến trên khoảng $I$
- Nếu $f^{\prime}(x)<0$ với mọi $x \in I$ thì hàm số $f(x)$ nghịch biến trên khoảng $I$
- Nếu $f^{\prime}(x)=0$ với mọi $x \in I$ thì hàm số $f(x)$ không đổi trên khoảng $I$
Chú ý:
Khoảng $I$ vừa trình bày có thể được thay bởi một đoạn hoặc nửa khoảng.
Lúc này, chúng ta phải bổ xung thêm giả thiết “hàm số liên tục trên đoạn hoặc nửa khoảng”
Chẳng hạn:
- Nếu hàm số $f(x)$ liên tục trên đoạn $[a; b]$ và có đạo hàm $f^{\prime}(x)>0$ trên khoảng $(a; b)$ thì hàm số $f(x)$ đồng biến trên đoạn $[a; b]$
- …
Ngoài cách diễn đạt bằng lời ra, chúng ta còn có thể diễn đạt khẳng định trên bằng bảng biến thiên.
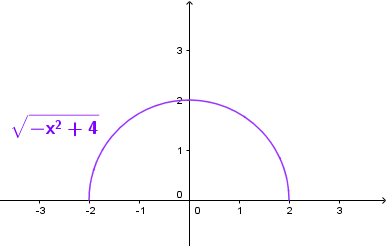
Ví dụ 1. Chứng minh rằng hàm số $f(x)=\sqrt{-x^2+4}$ nghịch biến trên đoạn $[0; 2]$
Lời giải:
Hàm số đã cho xác định trên đoạn $[0; 2]$
Với mọi $x_0 \in(0; 2)$ chúng ta có $\lim _{x \rightarrow x_0} f(x)=\lim _{x \rightarrow x_0} \sqrt{-x^2+4}=\sqrt{-x_0^2+4}=f\left(x_0\right)$ nên hàm số $f(x)$ liên tục trên khoảng $(0; 2)$
Ngoài ra, chúng ta còn có $\lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0^{+}} \sqrt{-x^2+4}=2=f(0)$ và $\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{-}} \sqrt{-x^2+4}=0=f(2)$
Suy ra hàm số đã cho liên tục trên đoạn $[0; 2]$
$f^{\prime}(x)=\frac{(-x^2+4)’}{2\sqrt{-x^2+4}}=\frac{-2x}{2\sqrt{-x^2+4}}=-\frac{x}{\sqrt{-x^2+4}}<0$ với mọi $x \in(0; 2)$
Vậy hàm số nghịch biến trên đoạn $[0; 2]$
Xem thêm:
#2. Các bước xét tính đơn điệu của hàm số
Như mình có nói ở đầu bài viết, việc xét tính đơn điệu của hàm số còn được gọi là xét chiều biến thiên của hàm số.
Mặt khác, việc xét chiều biến thiên của hàm số có đạo hàm có thể chuyển về việc xét dấu đạo hàm của nó.
Các bước xét tính đơn điệu của hàm số $y=f(x)$
- Bước 1. Tìm tập xác định của hàm số $y=f(x)$
- Bước 2. Tính đạo hàm $f^{\prime}(x)$ sau đó tìm các điểm $x_i(i=1,2, \ldots, n)$ mà tại đó đạo hàm bằng $0$ hoặc không xác định
- Bước 3. Sắp xếp các điểm $x_i$ theo thứ tự tăng dần và lập bảng biến thiên
- Bước 4. Dựa vào bảng biến thiên nêu kết luận về các khoảng đồng biến và nghịch biến của hàm số đã cho.
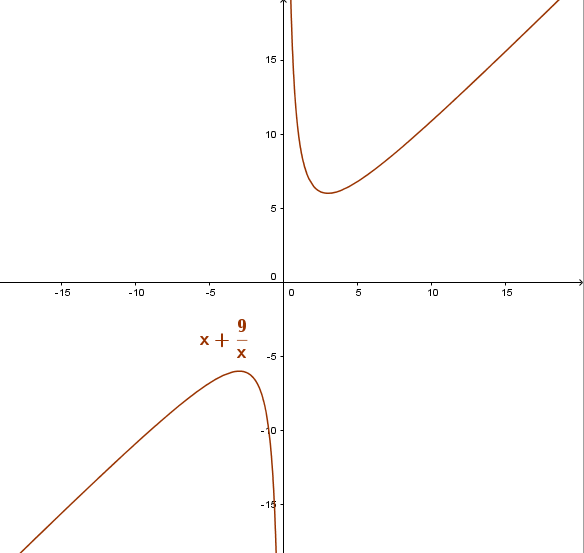
Ví dụ 2. Xét tính đơn điệu của hàm số $y=x+\frac{9}{x}$
Lời giải:
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Dễ thấy, hàm số đã cho có tập xác định $\mathbb{R} \backslash\{0\}$
$y^{\prime}=1-\frac{9}{x^2}=\frac{x^2-9}{x^2}$
$y^{\prime}=0 \Leftrightarrow \frac{x^2-9}{x^2}=0 \Leftrightarrow x=\pm 3$
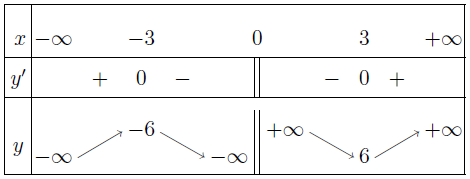
Chiều biến thiên của hàm số đã cho được trình bày trong bảng biến thiên.
Vậy hàm số đã cho:
- Đồng biến trên mỗi khoảng $(-\infty; -3)$ và $(3; +\infty)$
- Nghịch biến trên mỗi khoảng $(-3; 0)$ và $(0; 3)$
Xem thêm
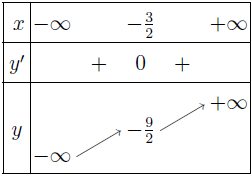
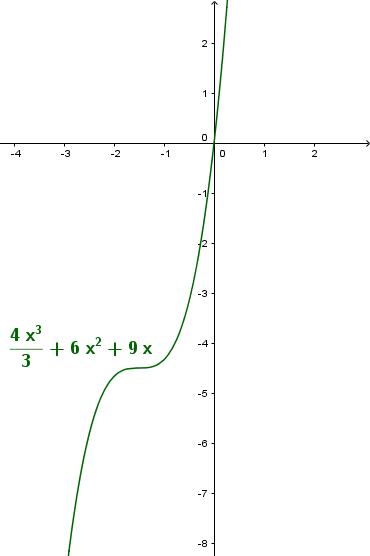
Ví dụ 3. Xét tính đơn điệu của hàm số $y=\frac{4 x^3}{3}+6 x^2+9 x$
Lời giải:
Vì hàm số đã cho là hàm đa thức nên có tập xác định $\mathbb{R}$
$y^{\prime}=4 x^2+12x+9=(2 x+3)^2$
$y^{\prime}=0$ với $x=-\frac{3}{2}$ và $y^{\prime}>0$ với mọi $x \neq -\frac{3}{2}$
Bảng biến thiên:
Suy ra hàm số đã cho đồng biến trên mỗi nửa khoảng $\left(-\infty ; \frac{3}{2}\right]$ và $\left[\frac{3}{2} ;+\infty\right)$
Vậy hàm số đã cho đồng biến trên $\mathbb{R}$
Nhận xét:
Giả sử hàm số $f(x)$ có đạo hàm trên khoảng $I$
Lúc này, nếu:
- $f^{\prime}(x) \geq 0$ với mọi $x \in I$
- Hoặc $f^{\prime}(x) \leq 0$ với mọi $x \in I$
- Và $f^{\prime}(x)=0$ chỉ tại một số hữu hạn điểm của $I$ thì..
Hàm số $f(x)$ đồng biến hoặc nghịch biến trên $I$
#3. Lời kết
Để xét tính đơn điệu của hàm số một cách dễ dàng thì ngoài các kiến thức vừa được trình bày ở trên thì bạn cũng nên xem lại các kiến thức sau:
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
